Ein Arbeitsmarktanalytiker untersucht die Beschäftigungstrends in drei Branchen über fünf Jahre (60 Monate). Der Analytiker führt eine ARIMA durch, um ein Modell für den Handel anzupassen.
- Öffnen Sie die Beispieldaten Beschäftigungstrends.MWX.
- Wählen Sie aus.
- Geben Sie im Feld Datenreihe die Spalte Handel ein.
- Geben Sie im Feld Autoregressiv unter Ohne Saisonkomponente den Wert 1 ein.
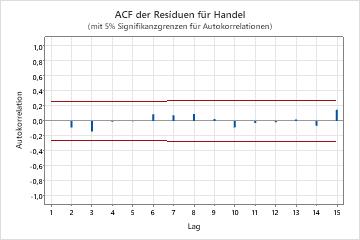
- Klicken Sie auf Grafiken, und wählen Sie ACF der Residuen aus.
- Klicken Sie auf OK.
Interpretieren der Ergebnisse
Der autoregressive Term weist einen p-Wert auf, der unterhalb des Signifikanzniveaus von 0,05
liegt. Der Analytiker schlussfolgert, dass sich der Koeffizient für den
autoregressiven Term statistisch von 0 unterscheidet, und behält den Term im Modell
bei. Alle p-Werte für die Ljung-Box-Chi-Quadrat-Statistiken sind größer als 0,05,
und keine der Korrelationen für die Autokorrelationsfunktion der Residuen ist
signifikant. Der Analytiker schlussfolgert, dass das Modell die Annahme erfüllt,
dass die Residuen unabhängig sind.
Schätzwerte bei jeder Iteration
| Iteration | SSE | Parameter | |
|---|---|---|---|
| 0 | 543,908 | 0,100 | 90,090 |
| 1 | 467,180 | -0,050 | 105,068 |
| 2 | 412,206 | -0,200 | 120,046 |
| 3 | 378,980 | -0,350 | 135,024 |
| 4 | 367,545 | -0,494 | 149,372 |
| 5 | 367,492 | -0,503 | 150,341 |
| 6 | 367,492 | -0,504 | 150,410 |
| 7 | 367,492 | -0,504 | 150,415 |
Endgültige Schätzwerte der Parameter
| Typ | Koef | SE Koef | t-Wert | p-Wert |
|---|---|---|---|---|
| AR 1 | -0,504 | 0,114 | -4,42 | 0,000 |
| Konstante | 150,415 | 0,325 | 463,34 | 0,000 |
| Mittelwert | 100,000 | 0,216 |
Anzahl der Beobachtungen: 60
Summen der Quadrate der Residuen
| DF | SS | MS |
|---|---|---|
| 58 | 366,733 | 6,32299 |
Modifizierte Box-Pierce (Ljung-Box) Chi-Quadrat-Statistik
| Lag | 12 | 24 | 36 | 48 |
|---|---|---|---|---|
| Chi-Quadrat | 4,05 | 12,13 | 25,62 | 32,09 |
| DF | 10 | 22 | 34 | 46 |
| p-Wert | 0,945 | 0,955 | 0,849 | 0,940 |

