Verwendungen der Exponentialverteilung zum Modellieren von Zuverlässigkeitsdaten
Die Exponentialverteilung ist eine einfache Verteilung mit nur einem Parameter, und sie wird häufig zum Modellieren von Zuverlässigkeitsdaten verwendet. Bei der Exponentialverteilung handelt es sich tatsächlich um einen Sonderfall der Weibull-Verteilung mit ß = 1.
- Mit Hilfe der Exponentialverteilung werden häufig elektronische Komponenten modelliert, bei denen ein Verschleiß in der Regel erst lange nach Ablauf der erwarteten Lebensdauer des Produkts einsetzt, in dem sie verbaut sind. Beispiele sind Komponenten von qualitativ hochwertigen Schaltkreisen wie Dioden, Transistoren, Widerstände und Kondensatoren.
- Die Exponentialverteilung wird auch als ausgezeichnetes Modell für die lange, „flache“ (relativ konstante) Periode des geringen Ausfallrisikos angesehen, die den mittleren Abschnitt der Badewannenkurve kennzeichnet. Diese Phase entspricht der Nutzungsdauer des Produkts und wird auch als Abschnitt der „intrinsischen Ausfälle“ der Kurve bezeichnet.
- Mit der Exponentialverteilung sollten jedoch keine mechanischen oder elektrischen Komponenten modelliert werden, bei denen Ermüdung, Korrosion oder Verschleiß bereits vor Ablauf der voraussichtlichen Lebensdauer des Produkts zu erwarten sind, z. B. Kugellager oder bestimmte Laser oder Glühfäden.
Die Exponentialverteilung zeichnet sich durch die wichtige Eigenschaft der „Erinnerungslosigkeit“ aus. „Erinnerungslosigkeit“ bedeutet, dass die verbleibende Lebensdauer einer Komponente unabhängig von ihrem gegenwärtigen Alter ist. Ein System, das der Abnutzung unterliegt und daher mit steigender Lebensdauer eine höhere Ausfallwahrscheinlichkeit hat, ist beispielsweise nicht „erinnerungslos“. Daher sollte diese Verteilung verwendet werden, wenn die Ausfallrate über die gesamte Lebensdauer des Produkts konstant ist. Die Anzahl der Ausfälle pro Zeiteinheit wird üblicherweise als Prozentsatz der Ausfälle pro Zeiteinheit angegeben, z. B. als Prozentsatz der Ausfälle pro tausend Stunden.
Beispiel 1: Transistoren
Für eine elektronische Komponente ist bekannt, dass sie über die gesamte Lebensdauer eines Produkts eine konstante Ausfallrate aufweist. Techniker erfassen den Ausfall der Komponente unter normalen Betriebsbedingungen.
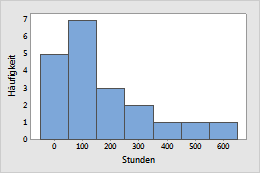
Beispiel 2: Glühfäden
Ein Glühlampenhersteller fertigt weißglühende Glühfäden, für die bei Normalbetrieb über einen längeren Zeitraum kein Verschleiß erwartet wird. Diese sollen für eine Betriebsdauer von 10 Jahren garantiert werden. Techniker setzen die Glühlampen erhöhten Stressbedingungen aus, um eine lang andauernde Nutzung zu simulieren, und zeichnen für jede Glühlampe die Monate bis zum Ausfall auf.
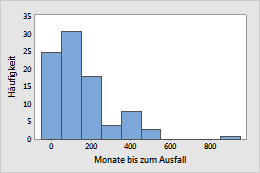
Dichtefunktion und Hazard-Funktion für die Exponentialverteilung
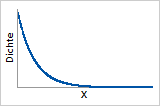
Dichtefunktion
Die Dichtefunktion zeigt, dass die Ausfalldaten rechtsschief sind.
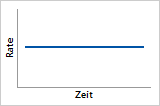
Hazard-Funktion
Die Hazard-Funktion zeigt, dass das Ausfallrisiko konstant ist.
