Überlebenswahrscheinlichkeiten
Die Zuverlässigkeitsfunktion R(t), die auch als Überlebensfunktion S(t) bezeichnet wird, stellt die Wahrscheinlichkeit dar, dass eine Einheit über einen bestimmten Zeitpunkt t hinaus überlebt.
Formel
R(t) = 1 – F(t)
Die Zuverlässigkeit eines seriellen Systems ist das Produkt der Zuverlässigkeitsfunktionen der Komponenten, da alle Komponenten überleben müssen, damit das System überlebt. Um die Zuverlässigkeit eines seriellen Systems mit unabhängigen Komponenten zu berechnen, multiplizieren Sie die Zuverlässigkeitsfunktionen sämtlicher Komponenten miteinander.
Notation
| Begriff | Beschreibung |
|---|---|
| F(t) | kumulative Verteilungsfunktion der ausgewählten Verteilung |
Konfidenzgrenzen für Überlebenswahrscheinlichkeiten
Die untere und die obere Konfidenzgrenze für die Überlebenswahrscheinlichkeiten werden durch die folgenden Formeln definiert:
Formel
wobei 
und 
(die Varianz der Überlebenswahrscheinlichkeiten) auf der Grundlage der Verteilung wie folgt definiert werden.
Kleinster Extremwert, normal, lognormal, logistisch, loglogistisch
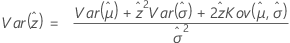
Lognormal mit 3 Parametern, loglogistisch mit 3 Parametern
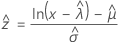
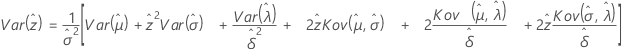
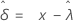
Weibull
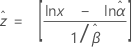
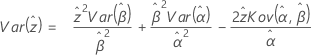
Weibull mit 3 Parametern
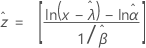
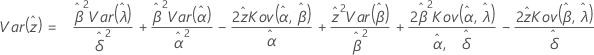
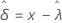
Exponential
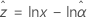
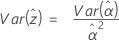
Exponential mit 2 Parametern
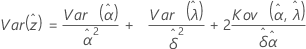
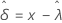
Notation
| Begriff | Beschreibung |
|---|---|
| zα | der 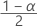 obere kritische Wert für die Standardnormalverteilung, wobei das Konfidenzniveau gleich 100α % ist. |
