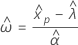Perzentile und Standardfehler der Perzentile
Perzentile sind Schätzwerte der Zeiten, zu denen ein bestimmter Prozentsatz der Grundgesamtheit ausgefallen ist. Standardmäßig zeigt Minitab in der verteilungsgebundenen Analyse Perzentiltabellen für gängige Perzentile an.
Die Standardfehler für die geschätzten Perzentile sind die Quadratwurzeln der Varianzen.
 ,
,  ,
,  ,
,  ,
,  ,
, 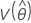 ,
, 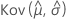 ,
, 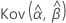 ,
, 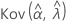 ,
, 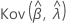 ,
, 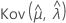 und
und 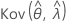 geben die Varianzen und Kovarianzen der MLEs von μ, σ, α, β, θ und λ an, die aus dem entsprechenden Element der Inverse der Fisher-Informationsmatrix entnommen wurden.
geben die Varianzen und Kovarianzen der MLEs von μ, σ, α, β, θ und λ an, die aus dem entsprechenden Element der Inverse der Fisher-Informationsmatrix entnommen wurden.
Die für die Schätzwerte der Perzentile und Varianzen für die einzelnen Verteilungen verwendeten Formeln lauten wie folgt:
Kleinster Extremwert
- Perzentil
-
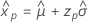
- Varianz
-

Weibull
- Perzentil
-

- Varianz
-
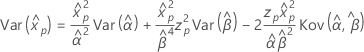
Weibull mit 3 Parametern
- Perzentil
-

- Varianz
-
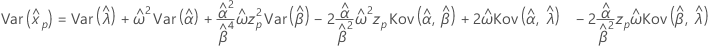
Exponential
- Perzentil
-

- Varianz
-

Exponential mit 2 Parametern
- Perzentil
-

- Varianz
-
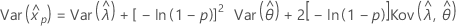
Normal
- Perzentil
-
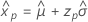
- Varianz
-

Lognormal
- Perzentil
-

- Varianz
-

Lognormal mit 3 Parametern
- Perzentil
-

- Varianz
-
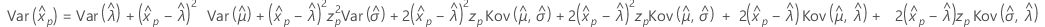
Logistisch
- Perzentil
-
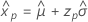
- Varianz
-

Loglogistisch
- Perzentil
-
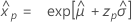
- Varianz
-

Loglogistisch mit 3 Parametern
- Perzentil
-

- Varianz
-

Notation
| Begriff | Beschreibung |
|---|---|
| zp |
inverse kumulative Verteilungsfunktion der Standardverteilung, ausgewertet bei p (dem p-ten Perzentil der Standardverteilung) |
Konfidenzgrenzen für Perzentile
| Verteilung | Konfidenzgrenzen |
|---|---|
|
Kleinster Extremwert Normal Logistisch |
 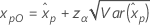 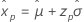 |
|
Weibull Exponential Lognormal Loglogistisch |
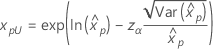 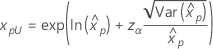 wobei |
|
Weibull mit 3 Parametern Exponential mit 2 Parametern Lognormal mit 3 Parametern Loglogistisch mit 3 Parametern |
Wenn λ < 0:  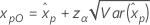 Wenn λ 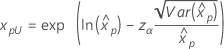 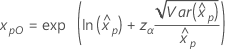 wobei |
Informationen zu den Berechnungen der Varianz des geschätzten xp finden Sie im Abschnitt „Perzentile und Standardfehler von Perzentilen“.
Notation
| Begriff | Beschreibung |
|---|---|
| zα | der 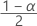 obere kritische Wert für die Standardnormalverteilung, wobei das Konfidenzniveau gleich 100α % ist. obere kritische Wert für die Standardnormalverteilung, wobei das Konfidenzniveau gleich 100α % ist. |