In diesem Thema
Parameterschätzwerte
Formel
| Verteilung | Parameter |
|---|---|
|
Kleinster Extremwert Normal Logistisch |
μ = Lage, σ = Skala, σ > 0 |
|
Lognormal Loglogistisch |
μ = Lage, μ > 0 σ = Skala, σ > 0 |
|
Lognormal mit 3 Parametern Loglogistisch mit 3 Parametern |
μ = Lage, μ > 0 σ = Skala, σ > 0 λ = Schwellenwert. |
|
Weibull |
α = Skala, α = exp(μ) β = Form, β = 1/σ |
|
Weibull mit 3 Parametern |
α = Skala, α = exp(μ) β = Form, β = 1/σ λ = Schwellenwert, |
|
Exponential |
θ = Skala, θ > 0 |
|
Exponential mit 2 Parametern |
θ = Skala, θ > 0 λ = Schwellenwert, |
Standardfehler der Parameterschätzwerte
Der Standardfehler ist die Standardabweichung des Parameterschätzwerts. Der Standardfehler stellt ein Maß für die Streuung in jedem Schätzwert dar.
, 
, 
, 
, 
und 
geben die Standardfehler der MLE von μ, σ, α, β, θ und λ an. Jeder Standardfehler wird als Quadratwurzel des entsprechenden Diagonalelements der Inverse der Fisher-Informationsmatrix berechnet.
Konfidenzgrenzen für die Parameterschätzwerte
Formel
| Verteilung | Parameter | Untere Konfidenzgrenze | Obere Konfidenzgrenze |
|---|---|---|---|
| Kleinster Extremwert, normal, logistisch, lognormal, loglogistisch | Lage, μ |
 |
 |
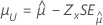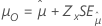| Skala, σ |
 |
 |
|
| Lognormal mit 3 Parametern, loglogistisch mit 3 Parametern | Lage, μ |
 |
 |
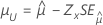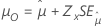| Skala, σ |
 |
 |
|
| Schwellenwert, λ |
 |
 |
|
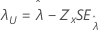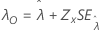| Weibull | Form, β |
 |
 |
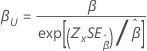| Skala, α |
 |
 |
|
|
Weibull mit 3 Parametern |
Form, β |
 |
 |
|
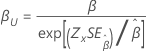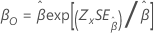Skala, α |
 |
 |
|
|
Schwellenwert, λ |
 |
 |
|
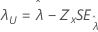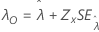| Exponential | Skala |
 |
 |
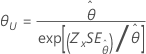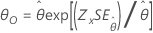| Exponential mit 2 Parametern | Skala, θ |
 |
 |
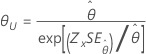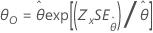| Schwellenwert, λ |
 |
 |
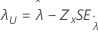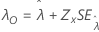Hinweis
Für einige Daten ist die Likelihood-Funktion unbeschränkt und liefert daher inkonsistente Schätzwerte für Verteilungen mit Schwellenwertparameter (z. B. die Exponentialverteilung mit 2 Parametern). Wenn dies zutrifft, kann die Varianz-Kovarianz-Matrix der geschätzten Parameter nicht numerisch bestimmt werden. In diesem Fall nimmt Minitab an, dass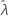 
fest ist, und dies resultiert in SE (
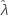) = 0. Die Obergrenze und die Untergrenze für 
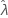ist gleich 
.
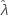Notation
| Begriff | Beschreibung |
|---|---|
| zx | der 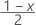 obere kritische Wert für die Standardnormalverteilung, wobei das Konfidenzniveau gleich 100x % und 0 < x < 1 ist. |
Log-Likelihood für Parameterschätzungen
Die Wahrscheinlichkeitsfunktionen für die verschiedenen Zensurschemata sind in Meeker et al. (2022)1.
