In diesem Thema
Mittelwert und Standardabweichung
Kleinster Extremwert
- Mittelwert
- μ – cσ
- Standardabweichung
-

Weibull
- Mittelwert
-
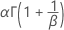
- Standardabweichung
-

Weibull mit 3 Parametern
- Mittelwert
-
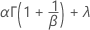
- Standardabweichung
-

Exponential
- Mittelwert
- θ
- Standardabweichung
- θ
Exponential mit 2 Parametern
- Mittelwert
- θ + λ
- Standardabweichung
- θ
Normal
- Mittelwert
- μ
- Standardabweichung
- σ
Lognormal
- Mittelwert
-
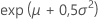
- Standardabweichung
-

Lognormal mit 3 Parametern
- Mittelwert
-
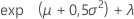
- Standardabweichung
-

Logistisch
- Mittelwert
- μ
- Standardabweichung
-

Loglogistisch
- Mittelwert
-

- Standardabweichung
-
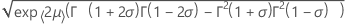
Loglogistisch mit 3 Parametern
- Mittelwert
-

- Standardabweichung
-
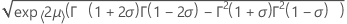
Notation
| Begriff | Beschreibung |
|---|---|
| c | Euler-Konstante (ungefähr gleich 0,5772) |
| Γ | Gamma-Funktion |
| μ | Lageparameter |
| β | Formparameter |
| σ | Skalenparameter |
| α | Skalenparameter (Weibull und Weibull mit 3 Parametern) |
| θ | Skalenparameter (exponential und exponential mit 2 Parametern) |
| λ | Schwellenwertparameter |
Median
Das 50. Perzentil. Weitere Informationen finden Sie im Thema „Perzentile“.
Quartile und Interquartilbereich
Erstes Quartil (Q1) = 25. Perzentil
Drittes Quartil (Q3) = 75. Perzentil
Interquartilbereich (IQR) = Q3 – Q1
Weitere Informationen finden Sie im Thema „Perzentile“.
MTTF
Bei der Zuverlässigkeitsanalyse ist die durchschnittliche Lebensdauer eines Produkts die mittlere Zeit bis zum Ausfall (MTTF).
Lognormale Verteilung
- MTTF
-

- Konfidenzintervall
-

Notation
| Begriff | Beschreibung |
|---|---|
 | Lageparameter |
| Begriff | Beschreibung |
|---|---|
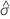 | Skalenparameter |
| Begriff | Beschreibung |
|---|---|
| zα/2 | Wert, der dem oberen α/2-Perzentil der Standardnormalverteilung entspricht |
| Begriff | Beschreibung |
|---|---|
| α | 1 – (Konfidenzniveau), wobei die Anzahl der Stichproben größer oder gleich 0 und kleiner oder gleich 1 sein muss |
| Begriff | Beschreibung |
|---|---|
| SEgi |
 |
Weibull-Daten
- MTTF
-
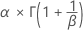
- Konfidenzintervall
-

Notation
| Begriff | Beschreibung |
|---|---|
| α | Skalenparameter |
| Begriff | Beschreibung |
|---|---|
| Γ | Gammafunktion bei r ausgewertet |
| Begriff | Beschreibung |
|---|---|
| β | Formparameter |
| Begriff | Beschreibung |
|---|---|
| g1 | log(MTTF) |
| Begriff | Beschreibung |
|---|---|
| SEgi |
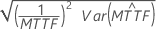 |
