In diesem Thema
Wahrscheinlichkeitsnetz
Verwenden Sie das Wahrscheinlichkeitsnetz, um zu beurteilen, wie gut die ausgewählte Verteilung an Ihre Daten angepasst ist. Wenn die Punkte nahe der Anpassungslinie liegen, können Sie annehmen, dass die Verteilung angemessen an die Daten angepasst ist.
- Die Punkte im Diagramm sind die unter Verwendung einer verteilungsfreien (also von keiner bestimmten Verteilung abhängigen) Methode geschätzten Perzentile. Wenn Sie mit dem Mauszeiger auf einen Datenpunkt zeigen, blendet Minitab die beobachtete Ausfallzeit und die geschätzte kumulative Wahrscheinlichkeit ein.
- Die Anpassungslinie (Mittellinie) beruht auf der angepassten Verteilung. Wenn Sie mit dem Mauszeiger auf die Anpassungslinie zeigen, blendet Minitab eine Tabelle mit Perzentilen für verschiedene Prozentsätze ein.
- Die linke Linie verbindet die Untergrenzen für die Konfidenzintervalle der einzelnen Perzentile. Die rechte Linie verbindet die Obergrenzen für die Konfidenzintervalle der einzelnen Perzentile.
Beispielausgabe
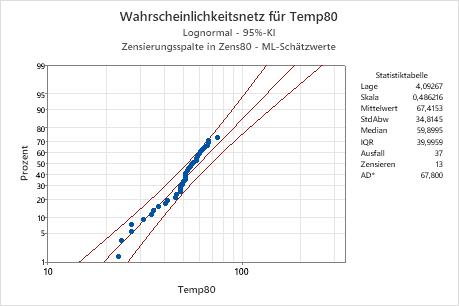
Interpretation
Für die Stichprobe in „Temp80“ der Motorwicklungsdaten scheinen die Punkte der Anpassungslinie zu folgen. Daher können Sie annehmen, dass die lognormale Verteilung für die Daten geeignet ist. Die Anpassungslinie beruht auf einer lognormalen Verteilung mit Lage = 4,09267 und Skala = 0,486216.
Überlebensdiagramm
Das Überlebensdiagramm stellt die Wahrscheinlichkeit dar, mit der eine Einheit bis zu einem bestimmten Zeitpunkt überlebt. Somit bildet das Überlebensdiagramm die Produktzuverlässigkeit über einen bestimmten Zeitraum ab.
- Die Mittellinie stellt die geschätzte Zuverlässigkeit über die Zeit dar.
- Mit der rechten Linie werden die Obergrenzen für die Zuverlässigkeit zu den einzelnen Zeitpunkten verbunden. Mit der linken Linie werden die Untergrenzen für die Zuverlässigkeit zu den einzelnen Zeitpunkten verbunden.
Wenn Sie mit dem Mauszeiger auf die Überlebenskurve zeigen, zeigt Minitab eine Tabelle mit Zeiten und Überlebenswahrscheinlichkeiten an.
Verwenden Sie dieses Diagramm nur, wenn die Verteilung ausreichend an die Daten angepasst ist. Wenn die Verteilung nicht ausreichend an die Daten angepasst ist, entstehen ungenaue Schätzwerte. Ermitteln Sie anhand einer Verteilungsidentifikation, eines Wahrscheinlichkeitsnetzes und der Maße für die Güte der Anpassung, ob die Verteilung ausreichend an die Daten angepasst ist.
Beispielausgabe
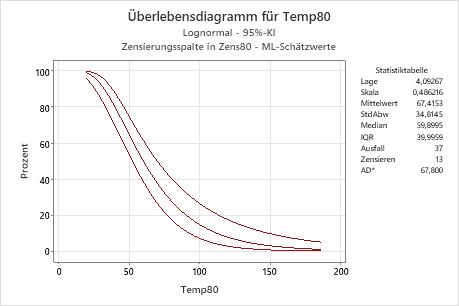
Interpretation
Für die Motorwicklungsdaten beläuft sich die Wahrscheinlichkeit, dass die Motorwicklungen bei einer Temperatur von 80 °C mindestens 50 Stunden überleben, auf ungefähr 60 %. Die Überlebensfunktion beruht auf der lognormalen Verteilung mit Lage = 4,09267 und Skala = 0,486216.
Diagramm der kumulierten Ausfälle
Das Diagramm der kumulierten Ausfälle zeigt den kumulierten Prozentsatz der Einheiten an, die bis zu einem bestimmten Zeitpunkt t ausfallen, um die Zuverlässigkeit des Produkts in Bezug auf dessen Ausfallzeit zu beschreiben. Die kumulierte Ausfallfunktion stellt 1 − Überlebensfunktion dar.
- Die Mittellinie stellt den geschätzten kumulierten Ausfallprozentsatz über die Zeit dar.
- Die rechte Linie verbindet die Untergrenzen der kumulierten Ausfallprozentsätze an den einzelnen Zeitpunkten. Die linke Linie verbindet die Obergrenzen der kumulierten Ausfallprozentsätze an den einzelnen Zeitpunkten.
Wenn Sie mit dem Mauszeiger auf die Kurve zeigen, blendet Minitab die kumulierte Ausfallwahrscheinlichkeit und die Ausfallzeit ein.
Verwenden Sie dieses Diagramm nur, wenn die Verteilung ausreichend an die Daten angepasst ist. Wenn die Verteilung nicht ausreichend an die Daten angepasst ist, entstehen ungenaue Schätzwerte. Ermitteln Sie anhand einer Verteilungsidentifikation, eines Wahrscheinlichkeitsnetzes und der Maße für die Güte der Anpassung, ob die Verteilung ausreichend an die Daten angepasst ist.
Beispielausgabe
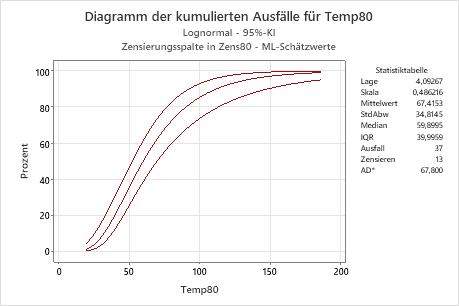
Interpretation
Für die Motorwicklungsdaten beläuft sich die Wahrscheinlichkeit, dass die Motorwicklungen bei einer Temperatur von 80 °C bis spätestens 70 Stunden ausfallen, auf ungefähr 60 %. Die kumulierte Ausfallfunktion beruht auf der lognormalen Verteilung mit Lage = 4,09267 und Skala = 0,486216.
Hazard-Diagramm
- Abnehmend: Die Einheiten fallen mit zunehmendem Alter mit geringerer Wahrscheinlichkeit aus. Ein abnehmender Hazard-Trend liegt meist in der Frühphase des Lebenszyklus eines Produkts vor.
- Konstant: Die Einheiten fallen mit gleichbleibender Rate aus. Ein konstanter Hazard-Trend liegt typischerweise während der eigentlichen Nutzungsdauer eines Produkts vor, in der Ausfälle nach zufälligem Muster auftreten.
- Zunehmend: Die Einheiten fallen mit zunehmendem Alter mit höherer Wahrscheinlichkeit aus. Ein zunehmender Hazard-Trend liegt meist in Spätphasen des Lebenszyklus eines Produkts vor, z. B. durch Abnutzung.
Die Form der Hazard-Funktion wird auf der Grundlage der Daten und der ausgewählten Verteilung ermittelt. Wenn Sie mit dem Mauszeiger auf die Hazard-Kurve zeigen, blendet Minitab eine Tabelle von Ausfallzeiten und Hazard-Raten ein.
Verwenden Sie dieses Diagramm nur, wenn die Verteilung ausreichend an die Daten angepasst ist. Wenn die Verteilung nicht ausreichend an die Daten angepasst ist, entstehen ungenaue Schätzwerte. Ermitteln Sie anhand einer Verteilungsidentifikation, eines Wahrscheinlichkeitsnetzes und der Maße für die Güte der Anpassung, ob die Verteilung ausreichend an die Daten angepasst ist.
Beispielausgabe
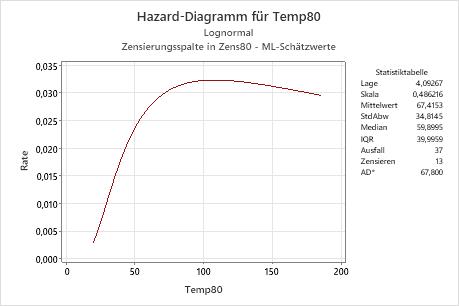
Interpretation
Für die Variable „Temp80“ der Daten zu Motorwicklungen basiert die Hazard-Funktion auf der lognormalen Verteilung mit Lage = 4,09267 und Skala = 0,486216. Bei einer Temperatur von 80 °C nimmt die Hazard-Rate bis ca. 100 Stunden zu und nimmt dann langsam ab.
Grafiken für mehrere Ausfallursachen
Für Daten mit mehreren Ausfallursachen zeigt Minitab Grafiken für jede einzelne Ausfallursache an.
- Verwenden Sie das Wahrscheinlichkeitsnetz, um zu beurteilen, wie gut die ausgewählte Verteilung an Ihre Daten angepasst ist. Wenn die Punkte nahe an der Anpassungslinie liegen, verwenden Sie diese Verteilung, um die Daten darzustellen.
- Verwenden Sie das Überlebensdiagramm, um die Wahrscheinlichkeit auszuwerten, mit der die Einheit bis zu einem bestimmten Zeitpunkt überlebt. Daher gibt das Überlebensdiagramm die Zuverlässigkeit des Produkts über einen bestimmten Zeitraum wieder.
- Verwenden Sie die Hazard-Funktion, um die Ausfallwahrscheinlichkeit als Funktion der Überlebensdauer einer Einheit darzustellen (die momentane Ausfallrate zu einem bestimmten Zeitpunkt t). Das Hazard-Diagramm zeigt den Trend der Ausfallrate über die Zeit an.
Beispielausgabe
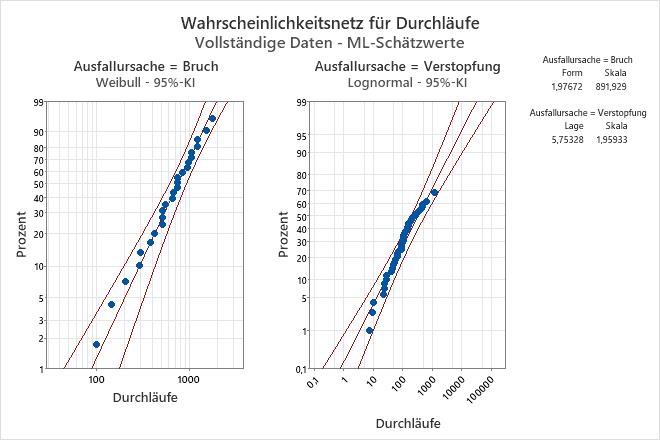
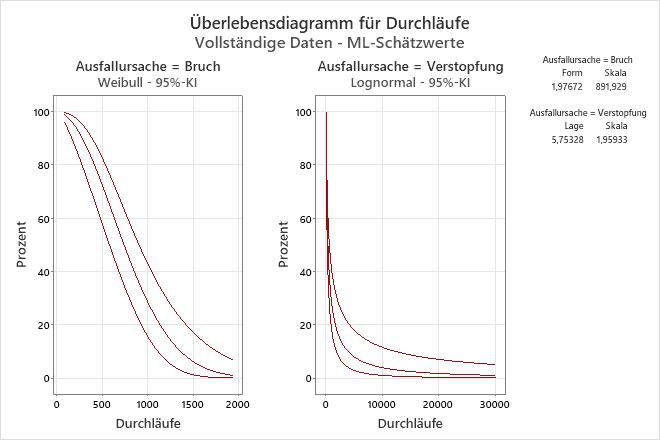
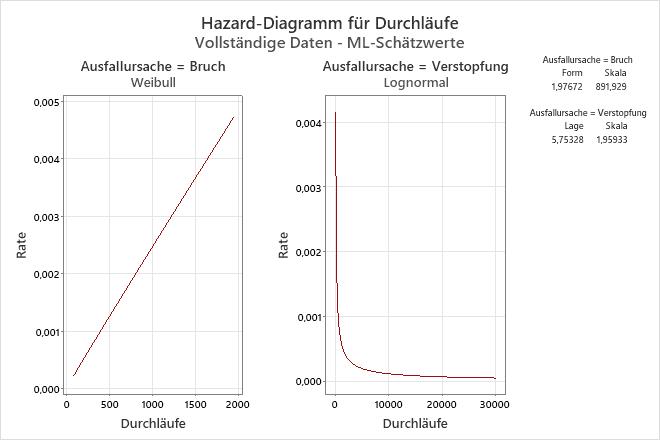
Interpretation
- Form = 1,97672 und Skala = 891,929 für die Brüche in den Sprüharmen
- Lage = 5,75328 und Skala = 1,95933 für Verstopfungen von Sprüharmen
Die Wahrscheinlichkeit, dass Sprüharme 200 Durchläufe ohne Bruch überleben, beträgt 95 %, und die Wahrscheinlichkeit, dass sie 1.500 Durchläufe ohne Verstopfung überleben, beläuft sich auf etwa 20 %.
Die Hazard-Rate für Brüche nimmt mit der Zeit leicht zu, während sie für Verstopfungen mit der Zeit abnimmt.
