Ein Zuverlässigkeitstechniker untersucht die Ausfallrate von Motorwicklungen in Turbinen, um die Zeitpunkte zu bestimmen, zu denen die Motorwicklungen ausfallen. Bei hohen Temperaturen können sich die Wicklungen zu schnell zersetzen.
- Die Zeiten, bei denen verschiedene Prozentsätze der Wicklungen ausfallen. Der Techniker ist insbesondere am 0,1-ten Perzentil interessiert.
- Den Prozentsatz der Wicklungen, die mehr als 70 Stunden überleben
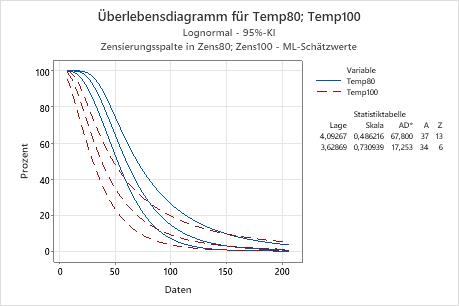
- Die Überlebensfunktion für die Motorwicklungen (wie in einem Überlebensdiagramm veranschaulicht)
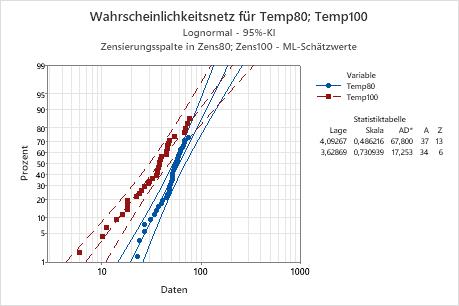
- Die Anpassungsgüte der Lognormalverteilung an die Daten (wie in einem Wahrscheinlichkeitsnetz veranschaulicht)
- Öffnen Sie die Beispieldaten Motorwicklungszuverlässigkeit.MWX.
- Wählen Sie aus.
- Geben Sie im Feld Variablen die Spalten Temp80 Temp100 ein.
- Wählen Sie im Feld Angenommene Verteilung den Wert Lognormal aus.
- Klicken Sie auf Zensieren. Geben Sie unter Zensierungsspalten verwenden die Spalten Zens80 Zens100 ein.
- Geben Sie im Feld Zensierungswert den Wert 0 ein. Klicken Sie auf OK.
- Klicken Sie auf Schätzen. Geben Sie im Feld Perzentile für diese zusätzlichen Prozentsätze schätzen den Wert 0,1 ein.
- Geben Sie im Feld Wahrscheinlichkeiten für diese Zeiten (Werte) schätzen den Wert 70 ein. Klicken Sie auf OK.
- Klicken Sie auf Grafiken. Wählen Sie Überlebensdiagramm aus.
- Klicken Sie in den einzelnen Dialogfeldern auf OK.
Interpretieren der Ergebnisse
Anhand der Perzentiltabelle kann der Techniker die Zeiten ermitteln, bei denen verschiedene Prozentsätze der Wicklungen ausfallen. Bei 80 °C fallen 1 % der Wicklungen nach spätestens 19,3281 Stunden aus. Die Werte für das 0,1-te Perzentil, das der Techniker für die Analyse angefordert hatte, werden ebenfalls in der Tabelle angezeigt. Bei 80 °C fallen 0,1 % der Wicklungen nach spätestens 13,3317 Stunden aus. Bei 100 °C fallen 0,1 % der Wicklungen nach spätestens 3,93505 Stunden aus. Somit verringert die Zunahme der Temperatur das Perzentil um einen Wert von ca. 9,5 Stunden.
Anhand der Tabelle der Überlebenswahrscheinlichkeiten kann der Techniker feststellen, für welchen Anteil der Wicklungen erwartet werden kann, dass sie länger als 70 Stunden überleben. Bei 80 °C ist für 37,43 % der Wicklungen zu erwarten, dass sie länger als 70 Stunden überleben. Bei 100 °C ist für 19,82 % der Wicklungen zu erwarten, dass sie länger als 70 Stunden überleben.
Der Techniker prüft anhand des Überlebensdiagramms die Überlebenswahrscheinlichkeiten über die Zeit, und mit Hilfe des Wahrscheinlichkeitsnetzes untersucht er, ob die lognormale Verteilung angemessen an die Daten angepasst ist.
- 80° C
- Variable: Temp80
Zensieren
Zensierungsinformation Anzahl Unzensierter Wert 37 Rechtszensierter Wert 13 Schätzmethode: Maximum-LikelihoodVerteilung: LognormalParameterschätzwerte
Normales 95,0%-KI Parameter Schätzwert Standardfehler Untergrenze Obergrenze Lage 4,09267 0,0719681 3,95161 4,23372 Skala 0,486216 0,0606247 0,380799 0,620816 Log-Likelihood = -181,625Güte der Anpassung
Anderson-Darling
(korrigiert)67,800 Merkmale der Verteilung
Normales 95,0%-KI Schätzwert Standardfehler Untergrenze Obergrenze Mittelwert (MTTF) 67,4153 5,55245 57,3656 79,2255 Standardabweichung 34,8145 6,79827 23,7435 51,0476 Median 59,8995 4,31085 52,0192 68,9735 Erstes Quartil (Q1) 43,1516 3,29526 37,1531 50,1186 Drittes Quartil (Q3) 83,1475 7,37690 69,8763 98,9392 Interquartilbereich (IQR) 39,9959 6,33317 29,3245 54,5505 Perzentiltabelle
Normales 95,0%-KI Prozent Perzentil Standardfehler Untergrenze Obergrenze 0,1 13,3317 2,51559 9,21026 19,2975 1 19,3281 2,83750 14,4953 25,7722 2 22,0674 2,92559 17,0178 28,6154 3 24,0034 2,97261 18,8304 30,5975 4 25,5709 3,00355 20,3126 32,1906 5 26,9212 3,02621 21,5978 33,5566 6 28,1265 3,04403 22,7506 34,7727 7 29,2276 3,05881 23,8074 35,8819 8 30,2501 3,07165 24,7910 36,9113 9 31,2110 3,08326 25,7170 37,8788 10 32,1225 3,09409 26,5962 38,7970 20 39,7837 3,20997 33,9646 46,5999 30 46,4184 3,41015 40,1936 53,6073 40 52,9573 3,75669 46,0833 60,8568 50 59,8995 4,31085 52,0192 68,9735 60 67,7517 5,15910 58,3584 78,6569 70 77,2958 6,45920 65,6184 91,0514 80 90,1863 8,58211 74,8412 108,678 90 111,696 12,8103 89,2100 139,849 91 114,958 13,5112 91,3052 144,738 92 118,610 14,3120 93,6288 150,255 93 122,759 15,2417 96,2426 156,581 94 127,565 16,3437 99,2372 163,979 95 133,276 17,6863 102,753 172,866 96 140,314 19,3873 107,026 183,955 97 149,477 21,6739 112,500 198,608 98 162,590 25,0764 120,175 219,977 99 185,634 31,3868 133,271 258,570 Tabelle der Überlebenswahrscheinlichkeiten
Normales 95,0%-KI Zeit Wahrscheinlichkeit Untergrenze Obergrenze 70 0,374299 0,263102 0,497141 - 100° C
- Variable: Temp100
Zensieren
Zensierungsinformation Anzahl Unzensierter Wert 34 Rechtszensierter Wert 6 Schätzmethode: Maximum-LikelihoodVerteilung: LognormalParameterschätzwerte
Normales 95,0%-KI Parameter Schätzwert Standardfehler Untergrenze Obergrenze Lage 3,62869 0,117785 3,39784 3,85955 Skala 0,730939 0,0919808 0,571172 0,935397 Log-Likelihood = -160,688Güte der Anpassung
Anderson-Darling
(korrigiert)17,253 Merkmale der Verteilung
Normales 95,0%-KI Schätzwert Standardfehler Untergrenze Obergrenze Mittelwert (MTTF) 49,1969 6,91761 37,3465 64,8076 Standardabweichung 41,3431 11,0416 24,4947 69,7806 Median 37,6636 4,43620 29,8995 47,4439 Erstes Quartil (Q1) 23,0044 2,95055 17,8910 29,5791 Drittes Quartil (Q3) 61,6643 8,49843 47,0677 80,7876 Interquartilbereich (IQR) 38,6600 7,24495 26,7759 55,8185 Perzentiltabelle
Normales 95,0%-KI Prozent Perzentil Standardfehler Untergrenze Obergrenze 0,1 3,93505 1,17289 2,19401 7,05767 1 6,87764 1,61698 4,33827 10,9034 2 8,39410 1,79420 5,52121 12,7619 3 9,52528 1,91113 6,42827 14,1144 4 10,4756 2,00146 7,20360 15,2338 5 11,3181 2,07658 7,89954 16,2162 6 12,0884 2,14187 8,54184 17,1076 7 12,8069 2,20031 9,14535 17,9343 8 13,4863 2,25376 9,71949 18,7129 9 14,1354 2,30344 10,2707 19,4544 10 14,7606 2,35025 10,8036 20,1667 20 20,3589 2,75256 15,6197 26,5362 30 25,6717 3,16619 20,1592 32,6916 40 31,2967 3,69496 24,8316 39,4451 50 37,6636 4,43620 29,8995 47,4439 60 45,3258 5,53158 35,6832 57,5740 70 55,2572 7,24447 42,7359 71,4473 80 69,6769 10,2054 52,2896 92,8456 90 96,1040 16,6968 68,3686 135,091 91 100,354 17,8420 70,8271 142,191 92 105,185 19,1727 73,5864 150,351 93 110,765 20,7464 76,7308 159,894 94 117,347 22,6502 80,3853 171,305 95 125,334 25,0242 84,7457 185,362 96 135,414 28,1141 90,1452 203,417 97 148,925 32,4050 97,2189 228,130 98 168,993 39,0628 107,427 265,843 99 206,255 52,1976 125,600 338,704 Tabelle der Überlebenswahrscheinlichkeiten
Normales 95,0%-KI Zeit Wahrscheinlichkeit Untergrenze Obergrenze 70 0,198233 0,107187 0,324816