Das Überlebensdiagramm stellt die Wahrscheinlichkeit dar, mit der eine Einheit bis zu einem bestimmten Zeitpunkt überlebt. Somit bildet das Überlebensdiagramm die Produktzuverlässigkeit über einen bestimmten Zeitraum ab. Auf der y-Achse wird die Überlebenswahrscheinlichkeit, auf der x-Achse die Zuverlässigkeitsmessung (Zeit, Anzahl von Kopien, gefahrene Kilometer) abgetragen.
Wenn Sie keine Verteilung auswählen (also eine verteilungsfreie Analyse durchführen), ist das Überlebensdiagramm eine Treppenfunktion, deren Stufen mit den Endpunkten jedes Intervalls übereinstimmen. In diesem Beispiel wird die Überlebensfunktion mit der versicherungsmathematischen Schätzmethode berechnet.
Wenn Sie mit dem Mauszeiger auf eine Stufe zeigen, zeigt Minitab die Überlebenswahrscheinlichkeit (y) bis zur dargestellten Zeit (x) an.
Beispielausgabe
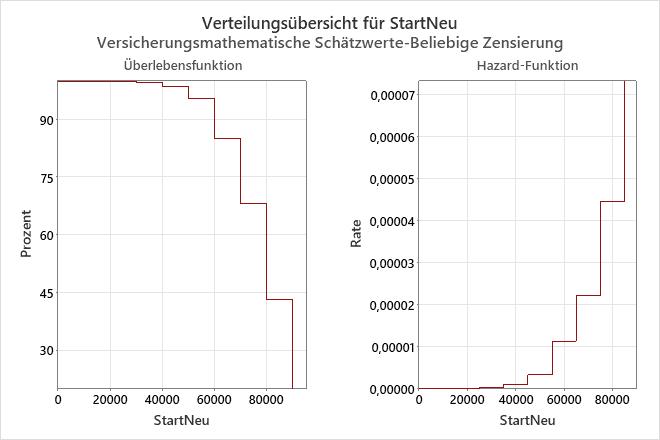
Interpretation
Auf der Grundlage der Daten für die neuen Schalldämpfer beläuft sich die Wahrscheinlichkeit, dass der neue Typ von Schalldämpfern 50.000 Meilen überlebt, auf ungefähr 0,95. Anders ausgedrückt besteht eine Wahrscheinlichkeit von 95 %, dass die Schalldämpfer 50.000 Meilen überleben.
