In diesem Thema
Wahrscheinlichkeitsnetz
- Diagrammpunkte: Die geschätzten Perzentile für die entsprechenden Wahrscheinlichkeiten eines geordneten Datensatzes.
- Anpassungslinie: Das erwartete Perzentil aus der Verteilung auf der Grundlage der Maximum-Likelihood-Schätzwerte für die Parameter.
- Konfidenzintervalle: Die Konfidenzintervalle für die Perzentile.
Da die Diagrammpunkte von keiner Verteilung abhängig sind, sind sie vor der Transformation für jedes erstellte Wahrscheinlichkeitsnetz gleich. Die Anpassungslinie unterscheidet sich jedoch je nach ausgewählter Verteilung. Mit Wahrscheinlichkeitsnetzen können Sie daher beurteilen, ob eine bestimmte Verteilung für die Daten passend ist. Je näher die Punkte an der Anpassungslinie liegen, desto besser ist im Allgemeinen die Anpassung.
Diagrammpunkte
- Median-Rang-Methode (Standardmethode)
- Modifizierte Kaplan-Meier-Methode
- Herd-Johnson-Methode
- Kaplan-Meier-Methode
Wenn die Daten gebundene Ausfallzeiten (identische Ausfallzeiten) enthalten, werden entweder alle Punkte (Standardeinstellung), der Durchschnitt (Median) oder das Maximum der gebundenen Punkte dargestellt. Wenn die Bindung Ausfälle und Aussetzungen einschließt, wird angenommen, dass die Ausfälle vor den Aussetzungen auftreten.
Jede dieser Methoden generiert verteilungsfreie Schätzwerte von F(t), der kumulativen Verteilungsfunktion für die Zufallsvariable T, die die Zeit bis zum Ausfall angibt.
Für eine Stichprobe von n Beobachtungen sei x(1), x(2),...,x(n) die Ordnungsstatistik, also die vom kleinsten zum größten Wert geordneten Daten. i ist dann der Rang der I-ten geordneten Beobachtung x(I). Die Formel für jede Methode lautet wie folgt:
Median-Rang (Benard-Methode)
Formel für unzensierte Daten
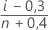
Formel für zensierte Daten
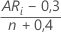
Kaplan-Meier modifiziert
Formel für unzensierte Daten
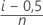
Formel für zensierte Daten
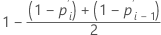
Herd-Johnson-Schätzung
Formel für unzensierte Daten

Formel für zensierte Daten
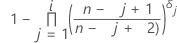
Kaplan-Meier-Produktlimitschätzung
Hinweis
Wenn die größte Beobachtung unzensiert ist, ergibt die Kaplan-Meier-Methode p = 1 für die größte unzensierte Beobachtung. In diesem Fall erhalten Sie mit dem Kaplan-Meier-Schätzwert für die größte Beobachtung eine Zahl, die im Diagramm nicht verwendet werden kann. Dieses Problem wird behoben, indem das größte p als 90 % der Distanz zwischen dem vorhergehenden p und 1 berechnet wird.
Hinweis
Für beliebig zensierte Daten schätzt Minitab die kumulativen Wahrscheinlichkeiten mit der Turnbull-Methode1.
Formel für unzensierte Daten

Formel für zensierte Daten
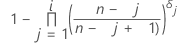
Notation
| Begriff | Beschreibung |
|---|---|
| i | Rang des Datenpunkts, wobei Bindungen aufeinanderfolgende Ränge zugewiesen werden |
| n | Anzahl der Beobachtungen in den Daten |
| δj | 0, wenn die j-te Beobachtung zensiert ist, oder 1, wenn die j-te Beobachtung unzensiert ist |
| ARi |
 |
| AR0 | entspricht 0 |
| p'i |
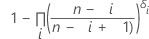 |
Anpassungslinie
- Minitab transformiert die x-Achse in eine Log-Skala, wenn Sie eine Weibull-Verteilung, Weibull-Verteilung mit 3 Parametern, Exponentialverteilung, lognormale Verteilung oder loglogistische Verteilung verwenden.
- Minitab transformiert die y-Achse standardmäßig in eine Prozentskala. Wenn Sie den Typ der y-Skala in eine Wahrscheinlichkeit ändern, transformiert Minitab die y-Achse in eine Skala für Wahrscheinlichkeiten.
| Verteilung | x-Koordinate | y-Koordinate |
|---|---|---|
| Kleinster Extremwert | Ausfallzeit | ln(–ln(1 – p)) |
| Weibull | ln(Ausfallzeit) | ln(–ln(1 – p)) |
| Weibull mit 3 Parametern | ln(Ausfallzeit – Schwellenwert) | ln(–ln(1 – p)) |
| Exponential | ln(Ausfallzeit) | ln(–ln(1 – p)) |
| Exponential mit 2 Parametern | ln(Ausfallzeit – Schwellenwert) | ln(–ln(1 – p)) |
| Normal | Ausfallzeit | Φ –1 (p) |
| Lognormal | ln(Ausfallzeit) | Φ –1 (p) |
| Lognormal mit 3 Parametern | ln(Ausfallzeit – Schwellenwert) | Φ –1 (p) |
| Logistisch | Ausfallzeit |
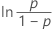 |
| Loglogistisch | ln(Ausfallzeit) |
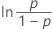 |
| Loglogistisch mit 3 Parametern | ln(Ausfallzeit – Schwellenwert) |
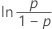 |
Notation
| Begriff | Beschreibung |
|---|---|
| Φ –1 | inverse kumulative Verteilungsfunktion der Standardnormalverteilung |
| ln(x) | natürlicher Logarithmus von x |
