Mit den Wahrscheinlichkeitsnetzen können Sie die Anpassungen von häufig verwendeten Verteilungen vergleichen und die Verteilung mit der besten Anpassung wählen. Wenn die Datenpunkte in einem bestimmten Wahrscheinlichkeitsnetz entlang einer relativ geraden Linie liegen, können Sie schlussfolgern, dass die Modellierung Ihrer Daten mit dieser Verteilung angemessen ist. Das heißt, die am besten angepasste Verteilung ist diejenige, bei der die Punkte am engsten an der Anpassungslinie anliegen.
Die Punkte im Diagramm sind die auf der Grundlage einer verteilungsfreien Methode geschätzten Perzentile. Wenn Sie mit dem Mauszeiger auf einen Datenpunkt zeigen, blendet Minitab die beobachtete Ausfallzeit und die geschätzte kumulative Wahrscheinlichkeit ein.
Die Linie beruht auf der angepassten Verteilung. In diesem Beispiel wurden die Weibull-Verteilung, die Lognormalverteilung, die Exponentialverteilung und die Normalverteilung angepasst. Wenn Sie mit dem Mauszeiger auf die Anpassungslinie zeigen, blendet Minitab eine Tabelle mit Perzentilen für verschiedene Prozentsätze ein.
Für die Maximum-Likelihood-Schätzmethode (MLE) wird von Minitab die Anderson-Darling-Statistik (kor) angezeigt, anhand derer die Anpassung jeder Verteilung bewertet wird.
Bei Verwendung der Schätzmethode der kleinsten Quadrate (LSXY) verwendet Minitab den Korrelationskoeffizienten nach Pearson. Dieser ist eine positive Zahl, die nicht größer als 1 sein kann. Je höher der Wert des Korrelationskoeffizienten, desto besser ist die Verteilung angepasst.
Hinweis
Weitere Informationen zum Interpretieren der Anderson-Darling-Statistik (kor) finden Sie unter „Güte der Anpassung“.
Beispielausgabe
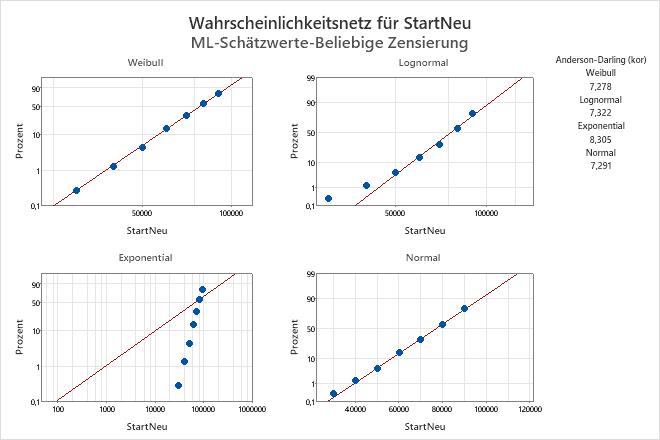
Interpretation
Für die Schalldämpferdaten geht aus den Wahrscheinlichkeitsnetzen hervor, dass die Weibull-Verteilung und die Normalverteilung gut an die Daten angepasst sind.
