Zuverlässigkeitsfunktion und inverse Zuverlässigkeitsfunktion
Kleinster Extremwert
- Zuverlässigkeit
-

- Inverse Zuverlässigkeit
-

Dabei gilt Folgendes:
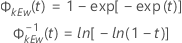
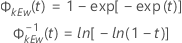
| Begriff | Beschreibung |
|---|---|
| t | Zeit |
| μ | Lageparameter |
| σ | Skalenparameter |
| ΦkEw(t) | kumulative Verteilungsfunktion der Verteilung des kleinsten Extremwerts |
| Φ–1kEw(t) | inverse kumulative Verteilungsfunktion der Verteilung des kleinsten Extremwerts |
Weibull
- Zuverlässigkeit
-
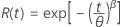
- Inverse Zuverlässigkeit
-

| Begriff | Beschreibung |
|---|---|
| t | Zeit |
| p | Wahrscheinlichkeit |
| β | Formparameter |
| θ | Skalenparameter |
Exponential
- Zuverlässigkeit
-

- Inverse Zuverlässigkeit
-
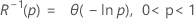
| Begriff | Beschreibung |
|---|---|
| t | Zeit |
| p | Wahrscheinlichkeit |
| θ | Mittelwertparameter |
Normal
- Zuverlässigkeit
-
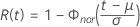
- Inverse Zuverlässigkeit
-

| Begriff | Beschreibung |
|---|---|
| t | Zeit |
| μ | Lageparameter |
| σ | Skalenparameter |
| Φnor(t) | kumulative Verteilungsfunktion der Normalverteilung |
| Φ–1nor(t) | inverse kumulative Verteilungsfunktion der Normalverteilung |
Lognormal
- Zuverlässigkeit
-

- Inverse Zuverlässigkeit
-

| Begriff | Beschreibung |
|---|---|
| t | Zeit |
| μ | Lageparameter |
| σ | Skalenparameter |
| Φnor(t) | kumulative Verteilungsfunktion der Normalverteilung |
| Φ–1nor(t) | inverse kumulative Verteilungsfunktion der Normalverteilung |
Logistisch
- Zuverlässigkeit
-
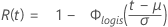
- Inverse Zuverlässigkeit
-
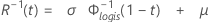
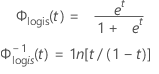
| Begriff | Beschreibung |
|---|---|
| t | Zeit |
| μ | Lageparameter |
| σ | Skalenparameter |
| Φlogis(t) | kumulative Verteilungsfunktion der logistischen Verteilung |
| Φ–1logis(t) | inverse kumulative Verteilungsfunktion der logistischen Verteilung |
Loglogistisch
- Zuverlässigkeit
-

- Inverse Zuverlässigkeit
-
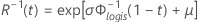
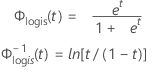
| Begriff | Beschreibung |
|---|---|
| t | Zeit |
| μ | Lageparameter |
| σ | Skalenparameter |
| Φlogis(t) | kumulative Verteilungsfunktion der logistischen Verteilung |
| Φ–1logis(t) | inverse kumulative Verteilungsfunktion der logistischen Verteilung |
Gleichung
Die Gleichung für einen m-Ausfälle-Testplan lautet wie folgt:

Notation
| Begriff | Beschreibung |
|---|---|
| α | Alpha (entspricht 1 – Konfidenzniveau) |
| R | Zuverlässigkeits- oder Überlebensfunktion zum Zeitpunkt t |
| N | minimale Anzahl der zu testenden Einheiten |
