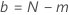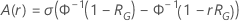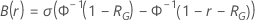Die Berechnungen für die Wahrscheinlichkeit, einen Testplan zu bestehen, hängen von der Verteilung ab, die die Fehler modelliert. Bei einer Verteilung mit Log-Lage und -Skala ist die Wahrscheinlichkeit eine Funktion des Verbesserungsverhältnisses. Bei einer Verteilung mit Lage und Skala ist die Wahrscheinlichkeit eine Funktion des Verbesserungsbetrags. Die Ausdrücke für die Formeln teilen sich in exakt zwei Fälle auf, die davon abhängen, ob Sie den Stichprobenumfang oder die Testzeit angeben.
Stichprobenumfang
 -Konfidenzniveau die folgende Gleichung:
-Konfidenzniveau die folgende Gleichung:
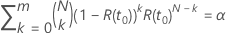
 hat die Lösung
hat die Lösung  der Gleichung die folgende Form:
der Gleichung die folgende Form:
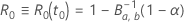
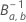 ist die inverse kumulative Verteilungsfunktion der Betaverteilung mit den folgenden Formparametern:
ist die inverse kumulative Verteilungsfunktion der Betaverteilung mit den folgenden Formparametern:
 invertieren Sie die Funktion
invertieren Sie die Funktion  . Die Inversion hängt von der Verteilungsfamilie ab.
. Die Inversion hängt von der Verteilungsfamilie ab.
- Familie mit Log-Lage und -Skala

- Familie mit Lage und Skala
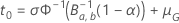
 und der Verbesserung abhängt:
und der Verbesserung abhängt:
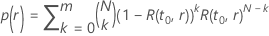
Dabei gilt: 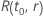 ist die Zuverlässigkeitsfunktion des Verteilungsmodells, ausgedrückt mit
ist die Zuverlässigkeitsfunktion des Verteilungsmodells, ausgedrückt mit  und
und 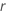 .
.
- Familie mit Log-Lage und -Skala

- Familie mit Lage und Skala
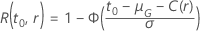
Die folgende Tabelle zeigt die Funktion von  für die Verteilungsfamilie und das Ziel des Tests:
für die Verteilungsfamilie und das Ziel des Tests:
| Zuverlässigkeitsziel | ||||
|---|---|---|---|---|
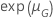 |
 |
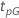 |
 |
|
| Log-Lage und -Skala |
 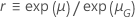 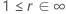 |
 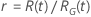  |
 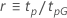 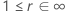 |
  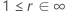 |
| Zuverlässigkeitsziel | ||||
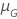 |
 |
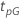 |
 |
|
| Lage und Skala |
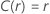  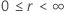 |
 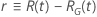  |
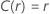  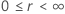 |
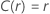 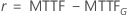 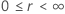 |
Beispiel für 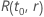 für die Weibull-Verteilung
für die Weibull-Verteilung
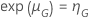 und einem gegebenen Stichprobenumfang hat die Wahrscheinlichkeit des Bestehens die folgende Form:
und einem gegebenen Stichprobenumfang hat die Wahrscheinlichkeit des Bestehens die folgende Form:
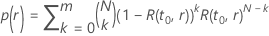
Dabei gilt Folgendes:

Testzeit
 -Konfidenzniveau die folgende Gleichung:
-Konfidenzniveau die folgende Gleichung:

 ) hat die Lösung der Gleichung
) hat die Lösung der Gleichung 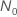 die folgende Form:
die folgende Form:

 ) gibt es keine Lösung in geschlossener Form. Meeker und Escobar (1998)1 geben die folgende ungefähre Lösung:
) gibt es keine Lösung in geschlossener Form. Meeker und Escobar (1998)1 geben die folgende ungefähre Lösung:
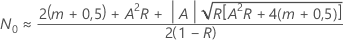
Dabei gilt Folgendes:

Minitab findet die exakte Lösung numerisch, wenn  .
.
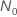 und der Verbesserung abhängt:
und der Verbesserung abhängt:
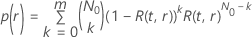
Dabei gilt: 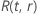 ist die Zuverlässigkeitsfunktion des Verteilungsmodells, ausgedrückt mit
ist die Zuverlässigkeitsfunktion des Verteilungsmodells, ausgedrückt mit  und
und 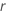 .
.
- Familie mit Log-Lage und -Skala

- Familie mit Lage und Skala
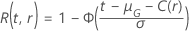
Die Funktion  hat die gleichen Definitionen wie bei Spezifikationen für den Test, die den Stichprobenumfang enthalten.
hat die gleichen Definitionen wie bei Spezifikationen für den Test, die den Stichprobenumfang enthalten.
Beispiel für 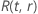 für die Weibull-Verteilung
für die Weibull-Verteilung
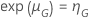 und einer gegebenen Testzeit hat die Wahrscheinlichkeit des Bestehens die folgende Form:
und einer gegebenen Testzeit hat die Wahrscheinlichkeit des Bestehens die folgende Form:
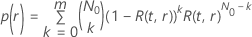
Dabei gilt Folgendes:

Notation
| Begriff | Beschreibung |
|---|---|
| N | Stichprobenumfang für das Design, wenn die Spezifikationen für den Test den Stichprobenumfang enthalten |
| m | Anzahl der Einheiten, die während des Tests ausfallen |
 | Signifikanzniveau, bei dem das Konfidenzniveau für den Test für Nachweise =  |
 | Skalenparameter |
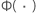 | kumulative Verteilungsfunktion der Standardverteilung für die ausgewählte Verteilung mit Log-Lage und -Skala bzw. Lage und Skala |
 | inverse kumulative Verteilungsfunktion der Standardverteilung für die ausgewählte Verteilung mit Log-Lage und -Skala bzw. Lage und Skala |
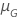 | Lageparameter für die Verteilung, die das Ziel des Tests erfüllt |
 | Formparameter der Weibull-Verteilung |
 | Testzeit, wenn die Spezifikationen für den Test den Stichprobenumfang enthalten |
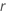 | Verbesserungsverhältnis für Verteilungen mit Log-Lage und -Skala oder Verbesserungsbetrag bei Verteilungen mit Lage und Skala |
 | Zuverlässigkeit zum Zeitpunkt t, die Ziel des Tests ist |
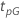 | Perzentil bei Prozent p, das Ziel des Tests ist |
 | mittlere Zeit bis zum Ausfall, die das Ziel des Tests ist |
 | Testzeit, wenn die Spezifikationen für den Test die Testzeit enthalten |
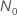 | Stichprobenumfang, wenn die Spezifikationen für den Test die Testzeit enthalten |