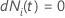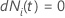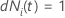| Begriff | Beschreibung |
|---|---|
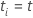
 | die unterschiedlichen, geordneten, Ereigniszeiten |
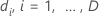 | die Anzahl der Ereignisse zum Zeitpunkt 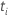 |
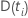 | die Menge aller Einheiten, die das Ereignis zu einem bestimmten Zeitpunkt
erleben 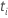 |
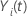 | eine Indikatorvariable mit dem Wert 1, wenn das Subjekt
i zum Zeitpunkt
t gefährdet ist, andernfalls 0, was dem 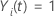 wenn wenn
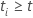 und
und 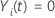 sonst
sonst |
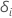 | ein Indikator dafür, ob das Subjekt
i zensiert wird, so dass 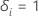 wenn Thema
i die Veranstaltung erlebt habe und
wenn Thema
i die Veranstaltung erlebt habe und 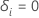 sonst
sonst |
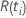 | das zu einem bestimmten Zeitpunkt festgelegte Risiko 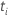 ,
das ist die Menge aller Stichprobeneinheiten, die vor der Zeit noch nicht
bestanden haben ,
das ist die Menge aller Stichprobeneinheiten, die vor der Zeit noch nicht
bestanden haben 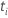 |
 | die Anzahl der Ereignisse für das Thema i bis einschließlich der Zeit t |
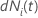 | die Änderung in  für Subjekt
i zum Zeitpunkt
t so, dass
für Subjekt
i zum Zeitpunkt
t so, dass
|
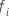 | der erste Ereigniszeit, zu dem sich Subjekt i in der Risikomenge befindet |
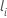 | der letzte Ereigniszeit, zu dem sich subjekt i in der Risikomenge befindet |
Cox-Snell-Residuen
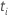 hat die folgende Form:
hat die folgende Form: 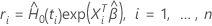
Dabei gilt:  ist der Breslow-Schätzwert der kumulativen Baseline-Gefahrenrate:
ist der Breslow-Schätzwert der kumulativen Baseline-Gefahrenrate:

 ist eine Schrittfunktion mit Sprüngen zu den beobachteten Ereigniszeiten. Die
Größe des Sprungs zum Zeitpunkt
ist eine Schrittfunktion mit Sprüngen zu den beobachteten Ereigniszeiten. Die
Größe des Sprungs zum Zeitpunkt 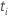 hat die folgende Form:
hat die folgende Form: 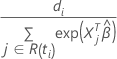

Für die Efron-Näherung hat der Cox-Snell-Rest folgende Form:
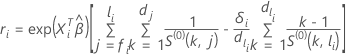
Dabei gilt: 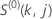 hat die folgende Form:
hat die folgende Form:
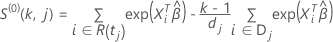
Für 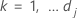
Dabei gilt: 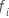 ist der erste Ereigniszeit, bei dem sich subjekt
i in der Risikomenge befindet und
ist der erste Ereigniszeit, bei dem sich subjekt
i in der Risikomenge befindet und 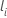 ist der letzte Ereigniszeitsatz, zu dem sich subjekt
i in der Risikomenge befindet.
ist der letzte Ereigniszeitsatz, zu dem sich subjekt
i in der Risikomenge befindet.
Martingale-Residuen

Dabei gilt:  ist der Cox-Snell-Rest und hängt von der Tie-Handling-Methode ab. Additiv
ist der Cox-Snell-Rest und hängt von der Tie-Handling-Methode ab. Additiv
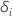 ist ein Indikator dafür, ob das Subjekt
i zensiert wird, so dass
ist ein Indikator dafür, ob das Subjekt
i zensiert wird, so dass 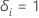 wenn Thema
ich die Veranstaltung erlebt habe und
wenn Thema
ich die Veranstaltung erlebt habe und
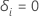 sonst
sonst
Abweichungsresiduen

Dabei gilt:  ist der Martingal-Rest für Subjekt
i.
ist der Martingal-Rest für Subjekt
i.
Schoenfeld-Residualvektor
Der Schoenfeld-Restvektor ist ein p-Komponentenvektor. Für das Subjekt i mit Ereigniszeit t hat der Schönfeld-Residualvektor folgende Form:
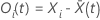
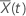 ist der gewichtete Durchschnitt der Kovariaten über das zum Zeitpunkt t
eingestellte Risiko. Der gewichtete Durchschnitt hat folgende Form:
ist der gewichtete Durchschnitt der Kovariaten über das zum Zeitpunkt t
eingestellte Risiko. Der gewichtete Durchschnitt hat folgende Form:
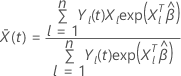
Dabei gilt: 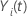 ist eine Indikatorvariable mit dem Wert 1, wenn das Subjekt
i zum Zeitpunkt
t gefährdet ist und andernfalls 0, was äquivalent ist
ist eine Indikatorvariable mit dem Wert 1, wenn das Subjekt
i zum Zeitpunkt
t gefährdet ist und andernfalls 0, was äquivalent ist 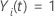 wenn
wenn
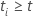 und
und 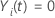 sonst.
sonst.
Wenn das Subjekt das Ereignis zum Zeitpunkt t nicht erlebt, enthält der Vektor fehlende Werte.
Die Berechnung des Schönfeld-Restvektors hängt von der Tie-Handling-Methode ab. Für die Breslow-Näherung hat der Schönfeld-Residualvektor folgende Form:
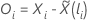
Dabei gilt Folgendes:
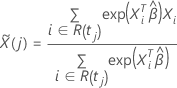
Für die Efron-Näherung hat der Schoenfeld-Residualvektor folgende Form:
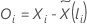
Dabei gilt Folgendes:
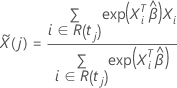
die Funktion 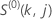 hat die gleiche Definition wie für das Cox-Snell-Residuum
hat die gleiche Definition wie für das Cox-Snell-Residuum
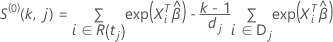
und
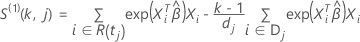
Für 
Skaliertes Schönfeld-Restvektor
Der skalierte Schönfeld-Residualvektor hat folgende Form:

Dabei gilt:  ist die
beobachtete Anzahl unzensierter Überlebenszeiten und
ist die
beobachtete Anzahl unzensierter Überlebenszeiten und 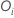 ist der Schoenfeld-Restvektor.
ist der Schoenfeld-Restvektor.
Score-Residualvektor
Die Berechnung des Score-Residualvektors hängt von der Näherungsmethode für Bindungen in den Ereigniszeiten ab. Für die Breslow-Näherung hat der Score-Residualvektor die folgende Form:
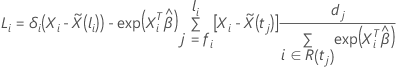
Dabei gilt Folgendes:
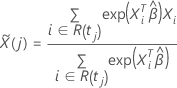
Für die Efron-Näherung hat der Score-Residualvektor die folgende Form:
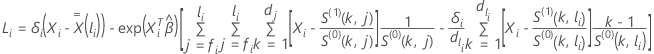
Dabei gilt: 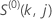 ,
,
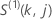 und
und  haben die gleichen Definitionen wie für den Schoenfeld-Residualvektor:
haben die gleichen Definitionen wie für den Schoenfeld-Residualvektor:
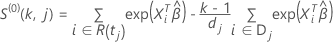
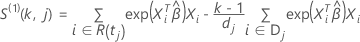
und
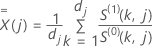
Für 
DFBeta
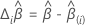

Dabei gilt: 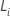 ist der Score-Restvektor. Weitere Einzelheiten zu den Schwellenwerten finden
Sie unter
ist der Score-Restvektor. Weitere Einzelheiten zu den Schwellenwerten finden
Sie unter  ,
gehe zu
Methoden und Formeln für die Koeffizienten und Regressionsgleichungen für Cox-Modell nur mit festen Prädiktoren anpassen.
,
gehe zu
Methoden und Formeln für die Koeffizienten und Regressionsgleichungen für Cox-Modell nur mit festen Prädiktoren anpassen.