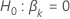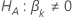Regressionsgleichung
Das semiparametrische Cox-Proportional-Hazards-Modell verwendet die
Prädiktorwerte für eine Person, 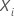 ,
um den Risiko-Score vorherzusagen,
,
um den Risiko-Score vorherzusagen, 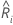 .
Die Regressionsgleichung weist die folgende allgemeine Form auf:
.
Die Regressionsgleichung weist die folgende allgemeine Form auf:

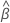 ist der vektor der geschätzten Koeffizienten Die geschätzten Koeffizienten
können Werte für Begriffe höherer Ordnung enthalten, z. B. die Quadrate
kontinuierlicher Prädiktoren. Der geschätzte Risiko-Score gilt für den gesamten
Zeitraum einer Studie und ist nicht zeitabhängig. In der Ausgabe hat die
Gleichung die folgende Form, in der eine separate Gleichung für verschiedene
Ebenen kategorialer Faktoren angezeigt wird:
ist der vektor der geschätzten Koeffizienten Die geschätzten Koeffizienten
können Werte für Begriffe höherer Ordnung enthalten, z. B. die Quadrate
kontinuierlicher Prädiktoren. Der geschätzte Risiko-Score gilt für den gesamten
Zeitraum einer Studie und ist nicht zeitabhängig. In der Ausgabe hat die
Gleichung die folgende Form, in der eine separate Gleichung für verschiedene
Ebenen kategorialer Faktoren angezeigt wird: 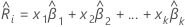
Koef
Lassen Sie die logpartielle Wahrscheinlichkeitsfunktion für das
Cox-Proportional-Hazards-Modell 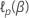 .
Der Vektor, der die Partial-Likelihood-Funktion maximiert,
.
Der Vektor, der die Partial-Likelihood-Funktion maximiert,
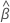 ,
gibt die geschätzten Koeffizienten für das Modell an. Finden
,
gibt die geschätzten Koeffizienten für das Modell an. Finden
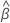 ,
setzen Sie die partiellen Ableitungen der logpartiellen
Wahrscheinlichkeitsfunktion auf Null und lösen Sie die Gleichungen für
,
setzen Sie die partiellen Ableitungen der logpartiellen
Wahrscheinlichkeitsfunktion auf Null und lösen Sie die Gleichungen für
 .
Minitab Statistical Software verwendet die Newton-Raphson-Iterationsmethode, um
die Gleichungen zu lösen. Siehe Murray (1972)1 für eine Beschreibung der newton-Raphson iterativen Methode.
.
Minitab Statistical Software verwendet die Newton-Raphson-Iterationsmethode, um
die Gleichungen zu lösen. Siehe Murray (1972)1 für eine Beschreibung der newton-Raphson iterativen Methode.
Der Vektor partieller Ableitungen der logpartiellen Wahrscheinlichkeitsfunktion hängt davon ab, ob die Antwortvariable gebundene Ereigniszeiten enthält. Wenn die Antwortvariable Bindungen enthält, verwendet die Schätzung entweder die Efron-Näherung oder die Breslow-Näherung. Wenn die Antwortvariable keine Bindungen hat, liefern alle 3 Methoden die gleichen Schätzungen. Je weniger Bindungen in den Daten enthalten sind, desto näher sind die Ergebnisse der beiden Approximationsmethoden. Je mehr Bindungen in den Daten sind, desto mehr verbessert sich die Efron-Näherung im Verhältnis zur Breslow-Näherung.
| Begriff | Beschreibung |
|---|---|
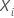 | der Vektor der kovariaten Werte, der der Stichprobeneinheit mit der
Ereigniszeit entspricht 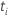 |
Daten ohne Bindung
| Begriff | Beschreibung |
|---|---|
 | die Anzahl der Ereigniszeiten |
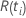 | das zu einem bestimmten Zeitpunkt festgelegte Risiko 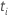 ,
bei der es sich um die Menge aller Stichprobeneinheiten handelt, die vor der
Zeit noch nicht fehlgeschlagen sind ,
bei der es sich um die Menge aller Stichprobeneinheiten handelt, die vor der
Zeit noch nicht fehlgeschlagen sind 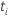 |
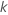 | eine Zählvariable für die Anzahl der Parameter im Modell,  wenn
wenn  ist die
Anzahl der Parameter im Modell ist die
Anzahl der Parameter im Modell |
Die partielle Wahrscheinlichkeitsfunktion für das Cox-Proportional-Hazards-Modell ohne Bindungen hat die folgende Form:
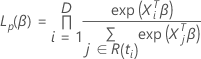
Die Verlustfunktion weist die folgende Form auf:
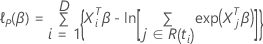
 hat die
folgende Form:
hat die
folgende Form: 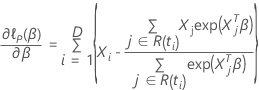
so dass die partielle Ableitung für einen bestimmten Koeffizienten,
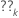 ,
hat die folgende Form:
,
hat die folgende Form:
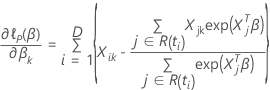
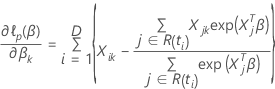
Daten mit Bindungen
| Begriff | Beschreibung |
|---|---|
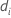 | die Anzahl der Ereignisse zum Zeitpunkt 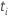 |
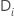 | Die Menge aller Beispieleinheiten, die das Ereignis zum Zeitpunkt haben
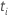 |
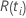 | das zu einem bestimmten Zeitpunkt festgelegte Risiko 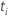 ,
das ist die Menge aller Stichprobeneinheiten, die vor der Zeit noch nicht
bestanden haben ,
das ist die Menge aller Stichprobeneinheiten, die vor der Zeit noch nicht
bestanden haben 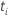 |

Efron-Approximation für Daten mit Bindungen
Die Verlustfunktion weist die folgende Form auf:
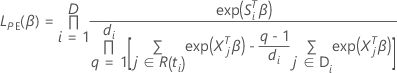
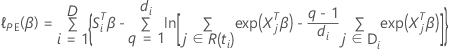
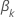 , hat die folgende Form:
, hat die folgende Form: 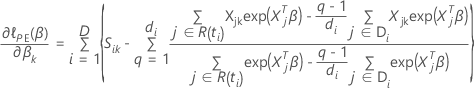
Breslow-Näherung für Daten mit Bindungen
Die Verlustfunktion weist die folgende Form auf:
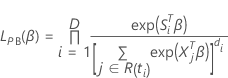
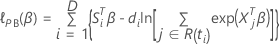
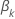 , hat die folgende Form:
, hat die folgende Form: 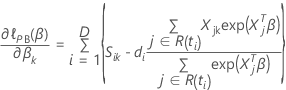
Kodierte Koeffizienten
Die Tabelle zeigt codierte Koeffizienten an, wenn die Analyse die kontinuierlichen Prädiktoren standardisiert. Um die codierten Koeffizienten zu finden, ersetzen Sie die standardisierten Prädiktoren in den vorhergehenden Gleichungen.
SE Koef
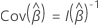
wobei die beobachtete Informationsmatrix,  hängt davon ab, ob die Antwortvariable gebundene Ereigniszeiten enthält. Wenn
die Antwortvariable Bindungen enthält, verwendet die Schätzung entweder die
Efron-Näherung oder die Breslow-Näherung. Wenn die Antwortvariable keine
Bindungen hat, liefern alle 3 Methoden die gleichen Schätzungen. Je weniger
Bindungen in den Daten enthalten sind, desto näher sind die Ergebnisse der
beiden Approximationsmethoden. Je mehr Bindungen in den Daten sind, desto mehr
verbessert sich die Efron-Näherung im Verhältnis zur Breslow-Näherung.
hängt davon ab, ob die Antwortvariable gebundene Ereigniszeiten enthält. Wenn
die Antwortvariable Bindungen enthält, verwendet die Schätzung entweder die
Efron-Näherung oder die Breslow-Näherung. Wenn die Antwortvariable keine
Bindungen hat, liefern alle 3 Methoden die gleichen Schätzungen. Je weniger
Bindungen in den Daten enthalten sind, desto näher sind die Ergebnisse der
beiden Approximationsmethoden. Je mehr Bindungen in den Daten sind, desto mehr
verbessert sich die Efron-Näherung im Verhältnis zur Breslow-Näherung.
Daten ohne Bindung
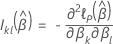
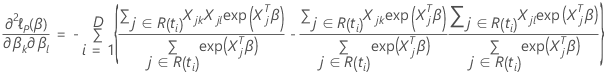
Efron-Approximation für Daten mit Bindungen
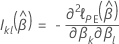
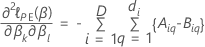
Dabei gilt Folgendes:
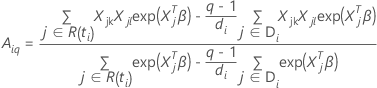
und
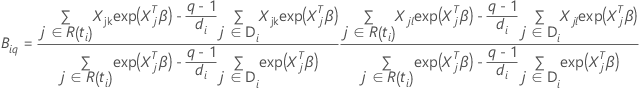
Breslow-Näherung für Daten mit Bindungen
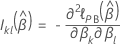
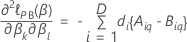
Dabei gilt Folgendes:
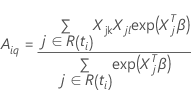
und
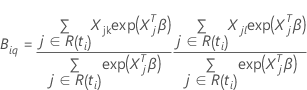
z-Wert
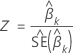
Dabei gilt:  ist der geschätzte Standardfehler des Koeffizienten
ist der geschätzte Standardfehler des Koeffizienten
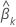 .
Die Werte von
.
Die Werte von  ist die positive Quadratwurzel des
k-ter diagonalen Elements von
ist die positive Quadratwurzel des
k-ter diagonalen Elements von  .
.
%-KI
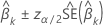
Dabei gilt: 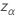 ist das obere
α Perzentilpunkt der Standardnormalverteilung.
ist das obere
α Perzentilpunkt der Standardnormalverteilung.
p-Wert

| Begriff | Beschreibung |
|---|---|
 | eine Zufallsvariable aus der Standardnormalverteilung |
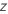 | die
Teststatistik für den 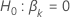 gegen die alternative hypothese
gegen die alternative hypothese 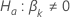 |
Stratifizierte proportionale Gefahrenmodelle
Für ein Modell, das eine kategoriale Variable mit s-Ebenen als Schichtungsvariable enthält, sind die Regressionskoeffizienten über Schichten hinweg konstant. Die Schätzung der Regressionskoeffizienten im geschichteten Modell hat den gleichen Prozess wie für das proportionale Gefahrenmodell ohne Schichtung. Für das geschichtete Modell hat die logpartielle Wahrscheinlichkeitsfunktion die folgende Form:

Dabei gilt: 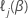 ist die log-partielle Wahrscheinlichkeit innerhalb der Schicht
j. Summieren Sie die Ableitungen über jede Schicht, um die partiellen
Wahrscheinlichkeitsgleichungen zu erhalten. Die Ableitungen über jede Schicht
sind die gleichen wie die Derivate für das proportionale Gefahrenmodell ohne
Schichtung. Die Breslow- und Efron-Methoden gelten entsprechend.
ist die log-partielle Wahrscheinlichkeit innerhalb der Schicht
j. Summieren Sie die Ableitungen über jede Schicht, um die partiellen
Wahrscheinlichkeitsgleichungen zu erhalten. Die Ableitungen über jede Schicht
sind die gleichen wie die Derivate für das proportionale Gefahrenmodell ohne
Schichtung. Die Breslow- und Efron-Methoden gelten entsprechend.