Es gibt zwei Bedingungen, die die Konvergenz der Maximum-Likelihood-Schätzwerte für die Koeffizienten verhindern: vollständige Trennung und quasi-vollständige Trennung.
Vollständige Trennung
Eine vollständige Trennung tritt auf, wenn eine lineare Kombination der Prädiktoren eine perfekte Prognose der Werte der Antwortvariablen liefert. Beispiel: Wenn im folgenden Datensatz x ≤ 4, dann y = 0. Wenn x > 4, dann y = 1.
| Y | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| X | 1 | 2 | 3 | 4 | 4 | 4 | 5 | 6 | 7 | 8 |
Quasi-vollständige Trennung
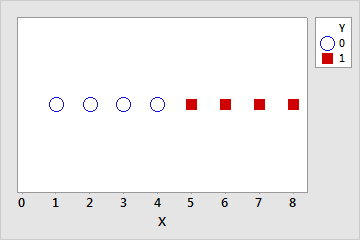
Eine quasi-vollständige Trennung ähnelt einer vollständigen Trennung. Die Prädiktoren liefern bei den meisten, nicht jedoch bei allen Werten eine perfekte Prognose der Werte der Antwortvariablen. Beispiel: Im folgenden Datensatz bei x = 4 ist für einen der Werte y = 1 und nicht 0. Wenn also x < 4, dann y = 0, wenn x > 4, dann y = 1, wenn jedoch x = 4, dann kann y sowohl 0 als auch 1 sein. Diese Überlappung im mittleren Bereich der Daten macht die Trennung quasi-vollständig.
| Y | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| X | 1 | 2 | 3 | 4 | 4 | 4 | 5 | 6 | 7 | 8 |

Ursachen und Abhilfe
Häufig tritt eine Trennung auf, wenn der Datensatz zu klein ist, um Ereignisse mit geringen Wahrscheinlichkeiten zu beobachten. Je mehr Prädiktoren das Modell enthält, desto wahrscheinlicher tritt eine Trennung auf, da die einzelnen Gruppen in den Daten kleinere Stichprobenumfänge aufweisen.
Minitab gibt zwar eine Warnung aus, wenn eine Trennung festgestellt wird, doch je mehr Prädiktoren das Modell enthält, desto schwieriger ist es, die Ursache der Trennung zu bestimmen. Das Einbinden von Wechselwirkungstermen im Modell erschwert dies zusätzlich.
- Vergrößern Sie die Datenmenge. Eine Trennung tritt häufig auf, wenn eine Kategorie oder ein Bereich eines Prädiktors mit nur einem Wert der Antwortvariablen vorhanden ist. Ein größerer Stichprobenumfang steigert die Wahrscheinlichkeit, dass unterschiedliche Werte für die Antwortvariable vorliegen.
- Untersuchen Sie die Bedeutung der Trennung. Eine vollständige bzw. quasi-vollständige Trennung kann zwar auf einen zu kleinen Stichprobenumfang hinweisen, sie kann jedoch auch wichtige Beziehungen aufzeigen. Wenn die tatsächliche Wahrscheinlichkeit eines Ereignisses auf einer bestimmten Stufe oder bei einer bestimmten Kombination von Stufen nahe 0 oder 1 liegt, ist diese Information wichtig.
- Erwägen Sie, ein alternatives Modell zu verwenden. Je mehr Terme im Modell enthalten sind, desto wahrscheinlicher tritt für mindestens eine Variable eine Trennung auf. Bei der Auswahl von Termen für das Modell können Sie prüfen, ob die Maximum-Likelihood-Schätzwerte durch Ausschließen eines Terms konvergieren. Wenn ein nützliches Modell vorhanden ist, in dem der Term nicht verwendet wird, können Sie die Analyse mit dem neuen Modell fortsetzen.
- Überprüfen Sie, ob Sie Kategorien in problematischen Variablen kombinieren können. Wenn Kategorien vorhanden sind, die sinnvollerweise kombiniert werden können, kann dies die Trennung im Datensatz u. U. aufheben. Angenommen, „Obst“ ist eine Variable im Modell. „Grapefruit“ weist keine Ereignisse auf, da eine kleinere Anzahl von Versuchen durchgeführt wurde. Durch Kombinieren von „Grapefruit“ und „Orangen“ in der Kategorie „Zitrusfrüchte“ wird die Trennung eliminiert.
Tabelle 1. Daten mit vollständiger Trennung Obst Ereignisse Versuche Grapefruit 0 10 Orangen 5 100 Äpfel 25 100 Bananen 40 100 Tabelle 2. Daten mit Überlappung Obst Ereignisse Versuche Zitrusfrüchte 5 110 Äpfel 25 100 Bananen 40 100 - Prüfen Sie, ob eine problematische kategoriale Variable eine aggregierte Variable ist. Wenn die Beziehung der nicht aggregierten Variablen mit der Antwortvariablen keine vollständige Trennung zur Folge hat, kann die Trennung durch Ersetzen der numerischen Daten beseitigt werden. Angenommen, „Beschäftigungsdauer“ ist eine aggregierte Variable im Modell. Wenn die Daten in 30-Tages-Intervallen vorliegen, enthält die niedrigste Stufe alle Ereignisse und die höchste Stufe keine Ereignisse, womit eine vollständige Trennung gegeben ist. Wenn im Modell stattdessen die Anzahl der Tage verwendet werden, beseitigt dies die Trennung.
Tabelle 3. Daten mit vollständiger Trennung Kategorien der Dauer Ereignisse Versuche 1–90 2 2 91–180 1 2 181–270 1 2 271–360 0 2 Genaue Dauer Ereignisse Versuche 45 1 1 60 1 1 95 1 1 176 0 1 185 0 1 241 1 1 280 0 1 299 0 1
Weiterführende Literatur
Weitere Informationen zur Trennung finden Sie in Albert und J. A. Anderson (1984), „On the existence of maximum likelihood estimates in logistic regression models“, Biometrika 71, 1, 1–10.
