Wie wirken sich Datenformate bei der binären logistischen Regression auf die Güte der Anpassung aus?

Bei der binären logistischen Regression wirkt sich das Datenformat auf die Interpretation des R² der Abweichung und des korrigierten R² der Abweichung aus. Beim Ereignis-/Versuchsformat stellt jeder beobachtete Wert die Wahrscheinlichkeit des Ereignisses für alle Versuche in dieser Zeile der Daten dar. In der Regel gilt diese Wahrscheinlichkeit für viele Versuche und liegt zwischen 0 and 1. Beim binären Antwort-/Häufigkeitenformat dagegen stellt jede Beobachtung in der Regel nur 1 Versuch dar. Der beobachtete Wert für einen einzelnen Versuch beträgt entweder 1 oder 0.

Im Allgemeinen führt der Unterschied bei den Datenformaten zu unterschiedlichen Gesamtabweichungen in den Daten. Bei Daten im Ereignis-/Versuchsformat bezieht sich die Abweichung auf die Diskrepanz zwischen den prognostizierten Wahrscheinlichkeiten und den beobachteten Wahrscheinlichkeiten. Beim binären Antwort-/Häufigkeitenformat bezieht sich die Abweichung auf die Diskrepanz zwischen den prognostizierten Wahrscheinlichkeiten und dem Ergebnis von 0 % oder 100 % für jeden Versuch. Das R² der Abweichung und das korrigierte R² der Abweichung sind für Daten im Ereignis-/Versuchsformat in der Regel höher.

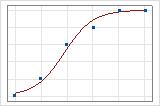
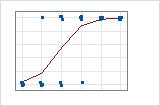
Ein grafische Darstellung verdeutlicht den Unterschied. In diesen Diagrammen stellen Symbole die Beobachtungen in den Daten dar, und die Kurve stellt die prognostizierten Werte im Modell dar. Bei Daten im Ereignis-/Versuchsformat liegen die Symbole nahe an der Linie. Der Wert des R² der Abweichung für die Daten im Ereignis-/Versuchsformat beträgt ungefähr 96 %. Das Modell prognostiziert die durchschnittlichen Wahrscheinlichkeiten sehr gut.

Bei Daten im binären Antwort-/Häufigkeitenformat liegen die Beobachtungen nur dann nahe an der prognostizierten Linie, wenn die Linie nahe an 0 % oder 100 % verläuft. Der Wert des R² der Abweichung für die Daten im binären Antwort-/Häufigkeitenformat beträgt ungefähr 56 %. Die Beziehung zwischen den prognostizierten Wahrscheinlichkeiten und den einzelnen Fällen ist weniger stark.

Bei der binären logistischen Regression wirkt sich das Datenformat auf die Zuverlässigkeit des Abweichungstests auf Güte der Anpassung aus. Der p-Wert für den Abweichungstest auf Güte der Anpassung nimmt in der Regel mit abnehmender Anzahl von Versuchen pro Zeile ab. Daten im binären Antwort-/Häufigkeitenformat weisen in der Regel weniger Versuche pro Zeile auf. Daher weist der Abweichungstest auf Güte der Anpassung bei Daten im binären Antwort-/Häufigkeitenformat wahrscheinlich auf eine schlechte Anpassung hin, auch wenn die Anpassung gut ist. Der Abweichungstest auf Güte der Anpassung weist auch dann fälschlicherweise auf eine wahrscheinlich schlechte Anpassung hin, wenn die Daten im Ereignis-/Versuchsformat vorliegen, aber die Zahl der Versuche pro Zeile klein ist.

Der Hosmer-Lemeshow-Test hängt nicht vom Format der Daten ab. Wenn die Daten nur wenige Versuche pro Zeile aufweisen, ist der Hosmer-Lemeshow-Test ein zuverlässigerer Indikator dafür, wie gut das Modell an die Daten angepasst ist.

Vergleichen Sie diese beiden Ergebnissätze für dieselben Daten in unterschiedlichen Formaten. Für diese Daten ist die Form des Modells korrekt. Die Informationen zur Antwortvariablen, die Koeffizienten und die Ergebnisse des Hosmer-Lemeshow-Tests stimmen überein. Die Schlussfolgerung für den Abweichungstest auf Güte der Anpassung hängt vom Datenformat ab.

In diesen Ergebnissen liegen die Daten im binären Antwort-/Häufigkeitenformat ohne Häufigkeitenspalte vor. Für die Analyse werden 500 Datenzeilen verwendet. Jede Zeile entspricht einem Versuch. Bei einem Signifikanzniveau von 0,05 zeigt der p-Wert für den Abweichungstest auf Güte der Anpassung an, dass das Modell schlecht angepasst ist. Dieser p-Wert führt zu der falschen Schlussfolgerung, dass das Modellformat nicht korrekt ist. Wenn Sie Daten im binären Antwort-/Häufigkeitenformat erfassen, ist der Abweichungstest auf Güte der Anpassung oft nicht zuverlässig.

In diesen Ergebnissen liegen die Daten im Ereignis-/Versuchsformat vor. Für die Analyse werden 5 Datenzeilen verwendet. Jede Zeile stellt 100 Versuche dar. Bei einem Signifikanzniveau von 0,05 weist der p-Wert für den Abweichungstest auf Güte der Anpassung nicht auf ein schlecht angepasstes Modell hin. Wenn Sie Daten im Ereignis-/Versuchsformat erfassen, ist der Abweichungstest auf Güte der Anpassung in der Regel zuverlässig.

Bei der binären logistischen Regression wirkt sich das Datenformat auf die Zuverlässigkeit des Pearson-Tests auf Güte der Anpassung aus. Die vom Pearson-Test verwendete Approximation an die Chi-Quadrat-Verteilung ist ungenau, wenn die erwartete Anzahl von Ereignissen pro Zeile klein ist. Daten im binären Antwort-/Häufigkeitenformat weisen in der Regel weniger Versuche pro Zeile auf. Daher ist der Pearson-Test auf Güte der Anpassung wahrscheinlich ungenau, wenn die Daten im binären Antwort-/Häufigkeitenformat vorliegen.

Der Hosmer-Lemeshow-Test hängt nicht vom Format der Daten ab. Wenn die Daten nur wenige Versuche pro Zeile aufweisen, ist der Hosmer-Lemeshow-Test ein zuverlässigerer Indikator dafür, wie gut das Modell an die Daten angepasst ist.

Vergleichen Sie diese beiden Ergebnissätze für dieselben Daten in unterschiedlichen Formaten. Für diese Daten ist die Form des Modells nicht korrekt. Das tatsächliche Modell enthält die Wechselwirkung zwischen x1 und x2. Die Informationen zur Antwortvariablen, die Koeffizienten und die Ergebnisse des Hosmer-Lemeshow-Tests stimmen überein. Die Schlussfolgerung aus dem Pearson-Test auf Güte der Anpassung hängt vom Datenformat ab.

In diesen Ergebnissen liegen die Daten im binären Antwort-/Häufigkeitenformat mit einer Häufigkeitenspalte vor. Für die Analyse werden 18 Datenzeilen verwendet. Jede Zeile stellt 250 Bernoulli-Versuche dar. Bei einem Signifikanzniveau von 0,05 zeigt der p-Wert für den Pearson-Test auf Güte der Anpassung an, dass das Modell an die Daten angepasst ist. Dieser p-Wert führt zu der falschen Schlussfolgerung, dass das Modell angemessen ist. Wenn Sie Daten im binären Antwort-/Häufigkeitenformat erfassen, ist der Pearson-Test auf Güte der Anpassung nicht zuverlässig.

In diesen Ergebnissen liegen die Daten im Ereignis-/Versuchsformat vor. Für die Analyse werden 9 Datenzeilen verwendet. Jede Zeile stellt 500 Versuche dar. Bei einem Signifikanzniveau von 0,05 zeigt der p-Wert für den Test auf Güte der Anpassung nach Pearson an, dass das Modell nicht an die Daten angepasst ist. Wenn Sie Daten im Ereignis-/Versuchsformat erfassen, ist der Pearson-Test auf Güte der Anpassung in der Regel zuverlässig.