Was ist die Regressionsanalyse?
Eine Regressionsanalyse generiert eine Gleichung, mit der die statistische Beziehung zwischen einem bzw. mehreren Prädiktoren und der Antwortvariablen beschrieben und neue Beobachtungen prognostiziert werden. Bei der linearen Regression wird im Allgemeinen die Schätzmethode der kleinsten Quadrate verwendet, mit der die Gleichung durch Minimieren der Summe der quadrierten Residuen abgeleitet wird.
Angenommen, Sie sind für einen Hersteller von Kartoffelchips tätig, der die Faktoren analysiert, die den Prozentsatz an zerkrümelten Kartoffelchips pro Behälter (Antwortvariable) vor der Auslieferung beeinflussen. Sie führen eine Regressionsanalyse durch und nehmen den Prozentsatz an Kartoffeln relativ zu den anderen Zutaten und die Frittiertemperatur (Grad Celsius) als die zwei Prädiktoren in das Modell auf. Die Ergebnisse werden in der folgenden Tabelle dargestellt.
Regressionsanalyse: Zerbrochene Chip vs. Prozent Kartoffe; Frittiertemperat
- Bei jedem Anstieg der Frittiertemperatur um 1 Grad Celsius wird erwartet, dass der Prozentsatz an zerkrümelten Kartoffelchips um 0,022 % steigt.
- Um den Prozentsatz an zerkrümelten Kartoffelchips für Einstellungen mit einer Kartoffelmenge von 0,5 (50 %) und einer Frittiertemperatur von 175 °C zu prognostizieren, berechnen Sie einen erwarteten Wert von 7,7 % zerkrümelten Kartoffelchips: 4,251 – 0,909 * 0,5 + 0,2231 * 175 = 7,70075.
- Das Vorzeichen der einzelnen Koeffizienten gibt die Richtung der Beziehung an.
- Koeffizienten stellen die mittlere Änderung der Antwortvariablen dar, wenn die Prädiktorvariable eine Änderung in Höhe einer Einheit aufweist und die anderen Prädiktoren im Modell auf konstanten Werten gehalten werden.
- Mit dem p-Wert der einzelnen Koeffizienten wird die Nullhypothese getestet, dass der Koeffizient gleich null ist (kein Effekt). Daher geben kleine p-Werte an, dass der entsprechende Prädiktor eine sinnvolle Erweiterung des Modells darstellt.
- Mit der Gleichung werden neue Beobachtungen auf der Grundlage gegebener Prädiktorwerte prognostiziert.
Hinweis
Modelle mit einem Prädiktor werden als einfache Regression bezeichnet. Modelle mit mehreren Prädiktoren werden als multiple lineare Regression bezeichnet.
Was ist die einfache lineare Regression?
Mit einer einfachen linearen Regression wird die lineare Beziehung zwischen zwei stetigen Variablen untersucht: einer Antwortvariablen (y) und einem Prädiktor (x). Wenn zwischen den beiden Variablen eine Beziehung besteht, kann anhand eines Prädiktorwerts ein Wert der Antwortvariablen prognostiziert werden. Dabei wird eine nicht zufällige Genauigkeit erreicht.
- Untersuchen, wie sich die Antwortvariable ändert, wenn sich die Prädiktorvariable ändert
- Prognostizieren des Werts einer Antwortvariablen (y) für jede beliebige Prädiktorvariable (x)
Was ist die multiple lineare Regression?
Bei der multiplen linearen Regression werden die linearen Beziehungen zwischen einer stetigen Antwortvariablen und mindestens zwei Prädiktoren untersucht.
Bei einer großen Anzahl von Prädiktoren sollten Sie vor dem Anpassen eines Regressionsmodells mit allen Prädiktoren die Prädiktoren ausschließen, die nicht signifikant in Beziehung zu den Werten der Antwortvariablen stehen. Diese können Sie über eine schrittweise Regression oder eine Regression der besten Teilmengen herausfiltern.
Was ist die normale Regression nach der Methode der kleinsten Quadrate?
Bei der normalen Regression der kleinsten Quadrate (OLS) wird die geschätzte Gleichung berechnet, indem die Gleichung ermittelt wird, die die Summe der quadrierten Distanzen zwischen den Datenpunkten der Stichprobe und den von der Gleichung prognostizierten Werten minimiert.
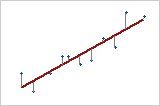
Antwort vs. Prädiktor
Bei einem Prädiktor (einfache lineare Regression) ist die Summe der quadrierten Distanzen von jedem Punkt zur Linie so klein wie möglich.
Annahmen für die OLS-Regression, die erfüllt sein sollten
- Das Regressionsmodell ist in den Koeffizienten linear. Bei Verwendung der kleinsten Quadrate kann die Krümmung durch Transformation der Variablen (statt der Koeffizienten) modelliert werden. Sie müssen die richtige Funktionsform angeben, um eine Krümmung angemessen modellieren zu können.
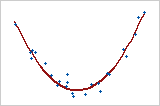
Quadratisches Modell
In diesem Fall wird die Prädiktorvariable X quadriert, um die Krümmung zu modellieren. y = bo + b1x + b2x2
- Die Residuen weisen den Mittelwert 0 auf. Durch Einbinden einer Konstanten im Modell wird der Mittelwert 0 erzwungen.
- Kein Prädiktor ist mit den Residuen korreliert.
- Die Residuen sind nicht miteinander korreliert (serielle Korrelation).
- Die Residuen weisen eine konstante Varianz auf.
- Keine Prädiktorvariable ist mit einer anderen Prädiktorvariablen perfekt korreliert (r=1). Nicht perfekte, aber hohe Korrelationen (Multikollinearität) werden möglichst ebenfalls vermieden.
- Die Residuen sind normalverteilt.
Da bei der OLS-Regression die besten Schätzwerte nur dann berechnet werden, wenn alle Annahmen erfüllt sind, ist es äußerst wichtig, diese zu testen. Zu den häufig verwendeten Methoden zählen die Untersuchung der Residuendiagramme, Tests auf fehlende Anpassung sowie das Betrachten der Korrelation zwischen den Prädiktoren mit Hilfe des Varianzinflationsfaktors (VIF).
