In diesem Thema
Varianzkomponenten
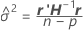
wobei 

Weitere Informationen zum Schätzen von θi finden Sie in [1].
Weitere Einzelheiten zur Notation finden Sie im Abschnitt „Methoden“.
Literaturhinweise
- Hemmerle, W. und Hartley, H. (1973). Computing Maximum Likelihood Estimates for the Mixed A.O.V. Model using the W transformation. Technometrics, 15(4): S. 819-831.
Standardfehler von Varianzkomponenten
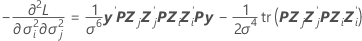
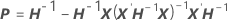
 Spalte, j = 1, …, c:
Spalte, j = 1, …, c:
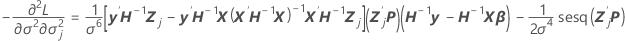

Diese Komponente entspricht zudem dem Wert der letzten Spalte und der  Zeile durch die Symmetrieeigenschaft der Varianz-Kovarianz-Matrix.
Zeile durch die Symmetrieeigenschaft der Varianz-Kovarianz-Matrix.

Die asymptotische Varianz-Kovarianz-Matrix für die Schätzwerte der Varianzkomponenten beläuft sich auf das Doppelte der Umkehrung der beobachteten Fisher-Informationsmatrix. Die Schätzwerte der Standardfehler sind die Quadratwurzeln der Diagonalelemente der Varianz-Kovarianz-Matrix. Die ersten c Diagonalelemente stehen für die Varianzkomponenten der Terme der Zufallseffekte. Das letzte Diagonalelement ist für die Fehlervarianzkomponente bestimmt.
Notation
| Begriff | Beschreibung |
|---|---|
 | Spur der Matrix  |
 | die Summe der Quadrate aller Elemente in der Matrix M |
Weitere Einzelheiten zur Notation finden Sie im Abschnitt „Methoden“.
Konfidenzintervalle für Varianzkomponenten
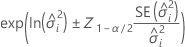
Notation
| Begriff | Beschreibung |
|---|---|
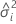 | Varianzkomponente für den i-ten Zufallsfaktor |
 | das 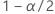 -te Quantil aus der Standardnormalverteilung -te Quantil aus der Standardnormalverteilung |
 | 1 − Konfidenzniveau |
z-Wert und p-Wert
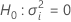
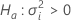


Notation
| Begriff | Beschreibung |
|---|---|
| z | Wert der inversen kumulativen Verteilungsfunktion für die Standardnormalverteilung |
Varianz-Kovarianz-Matrix
 Komponente der beobachteten Fisher-Informationsmatrix:
Komponente der beobachteten Fisher-Informationsmatrix:
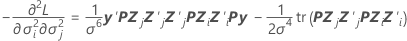

 Spalte, j = 1, …, c:
Spalte, j = 1, …, c:
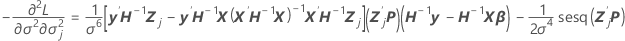

Diese Komponente entspricht zudem dem Wert der letzten Spalte und der  Zeile durch die Symmetrieeigenschaft der Varianz-Kovarianz-Matrix.
Zeile durch die Symmetrieeigenschaft der Varianz-Kovarianz-Matrix.

Notation
| Begriff | Beschreibung |
|---|---|
 | Spur der Matrix  |
Weitere Einzelheiten zur Notation finden Sie im Abschnitt „Methoden“.
