Methoden und Formeln für die Haltbarkeit für die Methode des angegebenen Prozentsatzes für Stabilitätsuntersuchung für feste Chargen

Das Modell mit Zeit, Charge und der Wechselwirkung Zeit*Charge

Wenn der Chargeneffekt und die Wechselwirkung Zeit*Charge im Modell enthalten sind, wird für die Anpassung der i-ten Charge zum Zeitpunkt x_ij das folgende Modell verwendet:

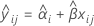
Um die Haltbarkeit zu ermitteln, setzen Sie die folgende Gleichung mit der unteren Spezifikationsgrenze gleich, und lösen Sie sie für die Zeit (x).

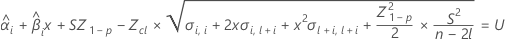
Dabei gilt Folgendes:

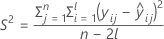
I = Gesamtzahl der Chargenstufen

n = Gesamtzahl der Werte der Antwortvariablen

X = Designmatrix für das Modell

Um eine sinnvolle Haltbarkeit zu berechnen, wertet Minitab drei Bedingungen aus. Zuerst ermittelt Minitab, ob der Mittelwert der Antwortvariablen zum Zeitpunkt = 0 statistisch größer als die untere Spezifikationsgrenze ist.

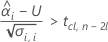
Zweitens ermittelt Minitab, ob der Mittelwert der Antwortvariablen über Zeit mit einer statistisch signifikanten Rate abnimmt.

Drittens ermittelt Minitab, ob es für den Quadratwurzelteil der quadratischen Gleichung eine Lösung in Form einer reellen Zahl gibt.

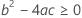
Dabei gilt Folgendes:

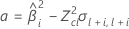
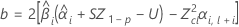
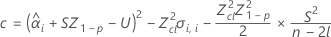
Wenn alle drei Bedingungen wahr sind, berechnet Minitab die Haltbarkeit. Verwenden Sie zum Berechnen der Haltbarkeit die quadratische Gleichung.

Das Modell mit Zeit und Charge

Wenn die Wechselwirkung Charge*Zeit nicht im Modell enthalten ist, sind die Steigungen für alle Chargen gleich. Bei der Anpassung für die i-te Charge zum Zeitpunkt x_ij wird das folgende Modell verwendet:

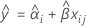
Um die Haltbarkeit zu ermitteln, setzen Sie die folgende Gleichung mit der unteren Spezifikationsgrenze gleich, und lösen Sie sie für die Zeit (x).

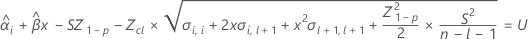
Dabei gilt Folgendes:

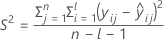
I = Gesamtzahl der Chargenstufen

n = Gesamtzahl der Werte der Antwortvariablen

X = Designmatrix für das Modell

Um eine sinnvolle Haltbarkeit zu berechnen, wertet Minitab drei Bedingungen aus. Zuerst ermittelt Minitab, ob der Mittelwert der Antwortvariablen zum Zeitpunkt = 0 statistisch größer als die untere Spezifikationsgrenze ist.

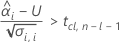
Zweitens ermittelt Minitab, ob der Mittelwert der Antwortvariablen über Zeit mit einer statistisch signifikanten Rate abnimmt.

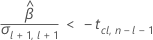
Drittens ermittelt Minitab, ob es für den Quadratwurzelteil der quadratischen Gleichung eine Lösung in Form einer reellen Zahl gibt.

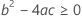
Dabei gilt Folgendes:

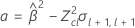
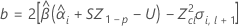
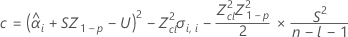
Wenn alle drei Bedingungen wahr sind, berechnet Minitab die Haltbarkeit. Verwenden Sie zum Berechnen der Haltbarkeit die quadratische Gleichung.

Das Modell mit Zeit

Wenn nur die Zeit im Modell enthalten ist, sind die Steigungen und Schnittpunkte mit der y-Achse für alle Chargen gleich. Bei der Anpassung zum Zeitpunkt x_ij wird das folgende Modell verwendet:

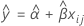
Um die Haltbarkeit zu ermitteln, setzen Sie die folgende Gleichung mit der unteren Spezifikationsgrenze gleich, und lösen Sie sie für die Zeit (x).

Dabei gilt Folgendes:

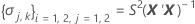
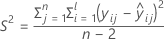
I = Gesamtzahl der Chargenstufen

n = Gesamtzahl der Werte der Antwortvariablen

X = Designmatrix für das Modell

Um eine sinnvolle Haltbarkeit zu berechnen, wertet Minitab drei Bedingungen aus. Zuerst ermittelt Minitab, ob der Mittelwert der Antwortvariablen zum Zeitpunkt = 0 größer als die untere Spezifikationsgrenze ist.

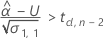
Zweitens ermittelt Minitab, ob der Mittelwert der Antwortvariablen über Zeit abnimmt.

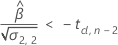
Drittens ermittelt Minitab, ob es für den Quadratwurzelteil der quadratischen Gleichung eine Lösung in Form einer reellen Zahl gibt.

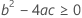
Dabei gilt Folgendes:

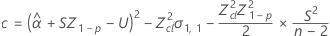
Wenn alle drei Bedingungen wahr sind, berechnet Minitab die Haltbarkeit. Verwenden Sie zum Berechnen der Haltbarkeit die quadratische Gleichung.

Notation

Begriff	Beschreibung
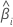	Steigung für die i-te Charge
Z	Wert der inversen kumulativen Wahrscheinlichkeitsfunktion aus der Standardnormalverteilung mit der gegebenen Wahrscheinlichkeit
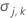	Varianz des geschätzten Parametervektors
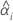	Schnittpunkt mit der y-Achse für die i-te Charge
S2	mittleres Fehlerquadrat
U	untere Spezifikationsgrenze
X	Designmatrix
i	Index, der die Charge angibt, für die die Haltbarkeit geschätzt wird
l	Anzahl der Stufen im Faktor Charge
n	Gesamtzahl der Werte der Antwortvariablen

Um die Berechnung der Haltbarkeit zu vereinfachen, ziehen Sie in Betracht, welches Modell Sie an die Daten anpassen.

Das Modell mit Zeit, Charge und der Wechselwirkung Zeit*Charge

Wenn der Chargeneffekt und die Wechselwirkung Zeit*Charge im Modell enthalten sind, wird für die Anpassung der i-ten Charge zum Zeitpunkt x_ij das folgende Modell verwendet:

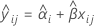
Um die Haltbarkeit zu ermitteln, setzen Sie die folgende Gleichung mit der oberen Spezifikationsgrenze gleich, und lösen Sie sie für die Zeit (x).

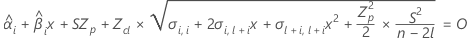
Dabei gilt Folgendes:

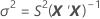
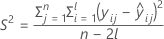
I = Gesamtzahl der Chargenstufen

n = Gesamtzahl der Werte der Antwortvariablen

X = Designmatrix für das Modell

Um eine sinnvolle Haltbarkeit zu berechnen, wertet Minitab drei Bedingungen aus. Zuerst ermittelt Minitab, ob der Mittelwert der Antwortvariablen zum Zeitpunkt = 0 statistisch kleiner als die obere Spezifikationsgrenze ist.

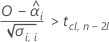
Zweitens ermittelt Minitab, ob der Mittelwert der Antwortvariablen über Zeit mit einer statistisch signifikanten Rate zunimmt.

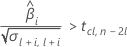
Drittens ermittelt Minitab, ob es für den Quadratwurzelteil der quadratischen Gleichung eine Lösung in Form einer reellen Zahl gibt.

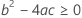
Dabei gilt Folgendes:

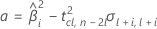
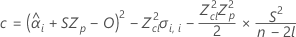
Wenn alle drei Bedingungen wahr sind, berechnet Minitab die Haltbarkeit. Verwenden Sie zum Berechnen der Haltbarkeit die quadratische Gleichung.

Das Modell mit Zeit und Charge

Wenn die Wechselwirkung Charge*Zeit nicht im Modell enthalten ist, sind die Steigungen für alle Chargen gleich. Bei der Anpassung für die i-te Charge zum Zeitpunkt x^ij wird das folgende Modell verwendet:

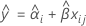
Um die Haltbarkeit zu ermitteln, setzen Sie die folgende Gleichung mit der oberen Spezifikationsgrenze gleich, und lösen Sie sie für die Zeit (x).

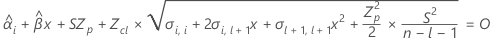
Dabei gilt Folgendes:

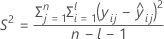
I = Gesamtzahl der Chargenstufen

n = Gesamtzahl der Werte der Antwortvariablen

X = Designmatrix für das Modell

Um eine sinnvolle Haltbarkeit zu berechnen, wertet Minitab drei Bedingungen aus. Zuerst ermittelt Minitab, ob der Mittelwert der Antwortvariablen zum Zeitpunkt = 0 statistisch kleiner als die obere Spezifikationsgrenze ist.

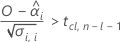
Zweitens ermittelt Minitab, ob der Mittelwert der Antwortvariablen über Zeit mit einer statistisch signifikanten Rate zunimmt.

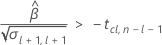
Drittens ermittelt Minitab, ob es für den Quadratwurzelteil der quadratischen Gleichung eine Lösung in Form einer reellen Zahl gibt.

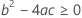
Dabei gilt Folgendes:

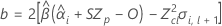
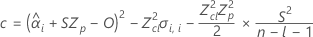
Wenn alle drei Bedingungen wahr sind, berechnet Minitab die Haltbarkeit. Verwenden Sie zum Berechnen der Haltbarkeit die quadratische Gleichung.

Das Modell mit Zeit

Wenn nur die Zeit im Modell enthalten ist, sind die Steigungen und Schnittpunkte mit der y-Achse für alle Chargen gleich. Bei der Anpassung zum Zeitpunkt x_ij wird das folgende Modell verwendet:

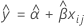
Um die Haltbarkeit zu ermitteln, setzen Sie die folgende Gleichung mit der oberen Spezifikationsgrenze gleich, und lösen Sie sie für die Zeit (x).

Dabei gilt Folgendes:

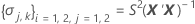
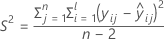
I = Gesamtzahl der Chargenstufen

n = Gesamtzahl der Werte der Antwortvariablen

X = Designmatrix für das Modell

Um eine sinnvolle Haltbarkeit zu berechnen, wertet Minitab drei Bedingungen aus. Zuerst ermittelt Minitab, ob der Mittelwert der Antwortvariablen zum Zeitpunkt = 0 kleiner als die obere Spezifikationsgrenze ist.

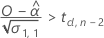
Zweitens ermittelt Minitab, ob der Mittelwert der Antwortvariablen über Zeit zunimmt.

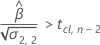
Drittens ermittelt Minitab, ob es für den Quadratwurzelteil der quadratischen Gleichung eine Lösung in Form einer reellen Zahl gibt.

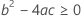
Dabei gilt Folgendes:

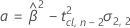
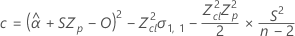
Wenn alle drei Bedingungen wahr sind, berechnet Minitab die Haltbarkeit. Verwenden Sie zum Berechnen der Haltbarkeit die quadratische Gleichung.

Notation

Begriff	Beschreibung
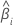	Steigung für die i-te Charge
Z	Wert der inversen kumulativen Wahrscheinlichkeitsfunktion aus der Standardnormalverteilung mit der gegebenen Wahrscheinlichkeit
	Varianz des geschätzten Parametervektors
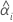	Schnittpunkt mit der y-Achse für die i-te Charge
S2	mittleres Fehlerquadrat
O	obere Spezifikationsgrenze
X	Designmatrix
i	Index, der die Charge angibt, für die die Haltbarkeit geschätzt wird
l	Anzahl der Stufen im Faktor Charge
n	Gesamtzahl der Werte der Antwortvariablen

Um die Berechnung der Bedingung dafür, wie und wann Minitab die Haltbarkeit berechnet, zu vereinfachen, ziehen Sie in Betracht, welches Modell Sie an die Daten anpassen.

Das Modell mit Zeit, Charge und der Wechselwirkung Zeit*Charge

Minitab wertet zwei Bedingungen aus, um zu bestimmen, ob eine sinnvolle Schätzung der Haltbarkeit vorhanden ist. Zuerst ermittelt Minitab, ob der Mittelwert der Antwortvariablen statistisch innerhalb der Spezifikationsgrenzen liegt.

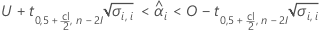
Dabei gilt Folgendes:

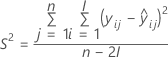
Begriff	Beschreibung
I	Gesamtzahl der Chargenstufen
n	Gesamtzahl der Werte der Antwortvariablen
X	Designmatrix für das Modell

Zweitens ermittelt Minitab, ob sich der Mittelwert der Antwortvariablen über Zeit mit einer statistisch signifikanten Rate ändert.

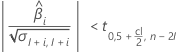
Wenn eine sinnvolle Schätzung vorhanden ist, bestimmt Minitab, ob der Mittelwert der Antwortvariablen über Zeit zu- oder abnimmt. Wenn die zweite Bedingung falsch ist, ist eine der folgenden Bedingungen war.

Wenn der Wert der Antwortvariablen über Zeit abnimmt, berechnet Minitab die Haltbarkeit in Bezug auf die untere Spezifikationsgrenze. Diese Formel gibt die Bedingung für einen abnehmenden Wert der Antwortvariablen an:

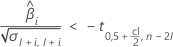
Wenn der Wert der Antwortvariablen über Zeit zunimmt, berechnet Minitab die Haltbarkeit in Bezug auf die obere Spezifikationsgrenze. Diese Formel gibt die Bedingung für einen zunehmenden Wert der Antwortvariablen an:

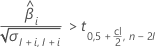
Wenn der Mittelwert der Antwortvariablen über Zeit abnimmt, berechnet Minitab die Haltbarkeit in Bezug auf die untere Spezifikationsgrenze. Anderenfalls berechnet Minitab die Haltbarkeit in Bezug auf die obere Spezifikationsgrenze.

Weitere Informationen zur Berechnung der Haltbarkeit im jeweiligen Fall finden Sie im entsprechenden Artikel:

Das Modell mit Zeit und Charge

Minitab wertet zwei Bedingungen aus, um zu bestimmen, ob eine sinnvolle Schätzung der Haltbarkeit vorhanden ist. Zuerst ermittelt Minitab, ob der Mittelwert der Antwortvariablen statistisch innerhalb der Spezifikationsgrenzen liegt.

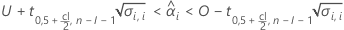
Dabei gilt Folgendes:

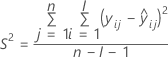
Begriff	Beschreibung
I	Gesamtzahl der Chargenstufen
n	Gesamtzahl der Werte der Antwortvariablen
X	Designmatrix für das Modell

Zweitens ermittelt Minitab, ob sich der Mittelwert der Antwortvariablen über Zeit mit einer statistisch signifikanten Rate ändert.

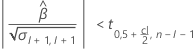
Wenn eine sinnvolle Schätzung vorhanden ist, bestimmt Minitab, ob die Haltbarkeit in Bezug auf die untere oder die obere Spezifikationsgrenze geschätzt werden soll.

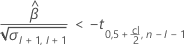
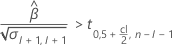
Weitere Informationen zur Berechnung der Haltbarkeit im jeweiligen Fall finden Sie im entsprechenden Artikel:

Das Modell mit Zeit

Minitab wertet zwei Bedingungen aus, um zu bestimmen, ob eine sinnvolle Schätzung der Haltbarkeit vorhanden ist. Zuerst ermittelt Minitab, ob der Mittelwert der Antwortvariablen statistisch innerhalb der Spezifikationsgrenzen liegt.

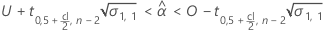
Dabei gilt Folgendes:

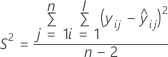
Begriff	Beschreibung
I	Gesamtzahl der Chargenstufen
n	Gesamtzahl der Werte der Antwortvariablen
X	Designmatrix für das Modell

Zweitens ermittelt Minitab, ob sich der Mittelwert der Antwortvariablen über Zeit mit einer statistisch signifikanten Rate ändert.

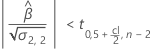
Wenn eine sinnvolle Schätzung vorhanden ist, bestimmt Minitab, ob die Haltbarkeit in Bezug auf die untere oder die obere Spezifikationsgrenze geschätzt werden soll.

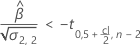
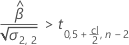
Weitere Informationen zur Berechnung der Haltbarkeit im jeweiligen Fall finden Sie im entsprechenden Artikel:

Notation

Begriff	Beschreibung
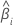	Steigung für die i-te Charge
I	Anzahl der Stufen im Faktor Charge
n	Anzahl der Zeilen in den Daten
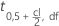	Wert der inversen kumulativen Verteilungsfunktion bei 0,5+cl/2 aus der t-Verteilung mit df Freiheitsgraden