In diesem Thema
Haltbarkeit für ein Modell mit Charge als Zufallsfaktor und nur einer unteren Spezifikationsgrenze
Um die Berechnung der Haltbarkeit zu vereinfachen, ziehen Sie in Betracht, ob das Modell die Wechselwirkung Zeit*Charge enthält.
Das Modell mit Zeit, Charge und der Wechselwirkung Zeit*Charge
Wenn der Chargeneffekt und die Wechselwirkung Zeit*Charge im Modell enthalten sind, wird für die Anpassung der i-ten Charge zum Zeitpunkt xij das folgende Modell verwendet:
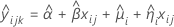
| Begriff | Beschreibung |
|---|---|
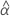 | geschätzter fester mittlerer Schnittpunkt mit der y-Achse für alle Chargen |
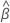 | geschätzte mittlere Steigung für alle Chargen |
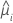 | geschätzter zufälliger mittlerer Schnittpunkt mit der y-Achse für die i-te Charge |
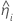 | geschätzte Steigung für die i-te Charge |
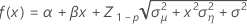
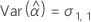

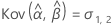


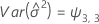
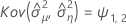
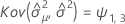
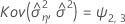
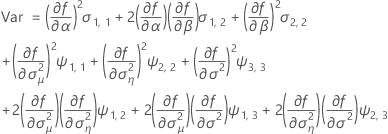
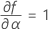
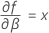

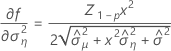

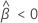

Minitab verwendet einen iterativen Algorithmus, um eine Lösung zu finden, die zwischen dem 0- und dem 10-fachen des größten Werts in der Zeit-Variablen liegt.
Das Modell mit Zeit und Charge
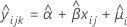
| Begriff | Beschreibung |
|---|---|
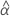 | geschätzter fester mittlerer Schnittpunkt mit der y-Achse für alle Chargen |
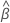 | geschätzte mittlere Steigung für alle Chargen |
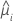 | geschätzter zufälliger mittlerer Schnittpunkt mit der y-Achse für die i-te Charge |
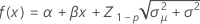
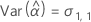

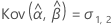

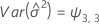
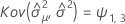
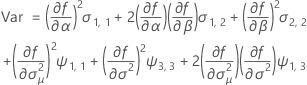
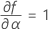
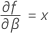
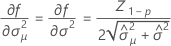
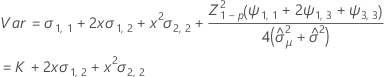
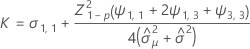

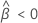
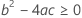


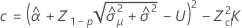


Notation
| Begriff | Beschreibung |
|---|---|
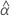 | geschätzter fester mittlerer Schnittpunkt mit der y-Achse für alle Chargen |
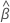 | geschätzte mittlere Steigung für alle Chargen |
| Z | Wert der inversen kumulativen Verteilungsfunktion |
| U | untere Spezifikationsgrenze |
| x | Haltbarkeit |
| p | Anteil des Produkts, der über der unteren Spezifikationsgrenze liegt |
| X | Designmatrix |
Haltbarkeit für ein Modell mit Charge als Zufallsfaktor und nur einer oberen Spezifikationsgrenze
Um die Berechnung der Haltbarkeit zu vereinfachen, ziehen Sie in Betracht, ob das Modell die Wechselwirkung Zeit*Charge enthält.
Das Modell mit Zeit, Charge und der Wechselwirkung Zeit*Charge
Wenn der Chargeneffekt und die Wechselwirkung Zeit*Charge im Modell enthalten sind, wird für die Anpassung der i-ten Charge zum Zeitpunkt xij das folgende Modell verwendet:
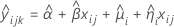
| Begriff | Beschreibung |
|---|---|
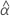 | geschätzter fester mittlerer Schnittpunkt mit der y-Achse für alle Chargen |
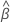 | geschätzte mittlere Steigung für alle Chargen |
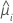 | geschätzter zufälliger mittlerer Schnittpunkt mit der y-Achse für die i-te Charge |
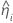 | geschätzte Steigung für die i-te Charge |

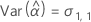

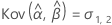


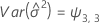
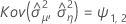
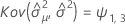
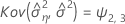
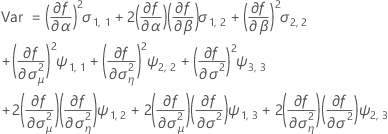
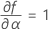
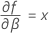

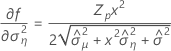

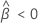
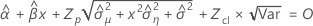
Minitab verwendet einen iterativen Algorithmus, um eine Lösung zu finden, die zwischen dem 0- und dem 10-fachen des größten Werts in der Zeit-Variablen liegt.
Das Modell mit Zeit und Charge
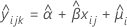
| Begriff | Beschreibung |
|---|---|
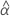 | geschätzter fester mittlerer Schnittpunkt mit der y-Achse für alle Chargen |
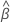 | geschätzte mittlere Steigung für alle Chargen |
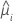 | geschätzter zufälliger mittlerer Schnittpunkt mit der y-Achse für die i-te Charge |
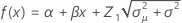
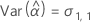

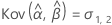

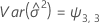
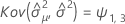
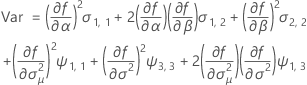
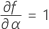
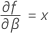
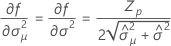
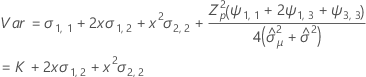
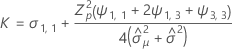

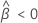
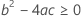


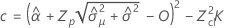
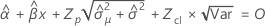

Notation
| Begriff | Beschreibung |
|---|---|
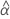 | geschätzter fester mittlerer Schnittpunkt mit der y-Achse für alle Chargen |
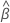 | geschätzte mittlere Steigung für alle Chargen |
| Z | Wert der inversen kumulativen Verteilungsfunktion |
| U | untere Spezifikationsgrenze |
| x | Haltbarkeit |
| p | Anteil des Produkts, der über der unteren Spezifikationsgrenze liegt |
| X | Designmatrix |
Beide Grenzen
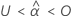
Wenn eine sinnvolle Schätzung vorhanden ist, bestimmt Minitab, ob die Haltbarkeit in Bezug auf die untere oder die obere Spezifikationsgrenze geschätzt werden soll.
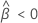

Weitere Informationen zur Berechnung der Haltbarkeit im jeweiligen Fall finden Sie im Abschnitt, der die Berechnung bei nur einer vorhandenen Spezifikationsgrenze beschreibt. Um die Haltbarkeit zu berechnen, wenn zwei Grenzen für die Berechnungen vorhanden sind, ändern Sie Zcl und Z0,95 in Z0,5+cl/2.
Notation
| Begriff | Beschreibung |
|---|---|
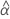 | geschätzter fester mittlerer Schnittpunkt mit der y-Achse für alle Chargen |
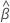 | geschätzte mittlere Steigung für alle Chargen |
| cl | Konfidenzniveau |
