In diesem Thema
Das gemischte Modell und Log-Likelihood
Die allgemeine Form des gemischten Modells
Modelle mit gemischten Effekten enthalten sowohl feste als auch Zufallseffekte. Die allgemeine Form des gemischten Modells lautet:
y = Xβ + Z1μ1 + Z2μ2 + ... + Zcμc + ε
Notation
| Begriff | Beschreibung |
|---|---|
| y | (n x 1)-Vektor von Werten der Antwortvariablen |
| x | (n x p)-Designmatrix für die festen Effekte, p ≤ n |
| Zi | (n x mi)-Designmatrix für den i-ten Zufallseffekt im Modell |
| β | ein (p x 1)-Vektor von unbekannten Parametern |
| μi | ein (mi x 1)-Vektor von unabhängigen Variablen aus N(0, σ2i) |
| ε | ein (n x 1)-Vektor von unabhängigen Variablen aus N(0, σ2i) |
| c | Anzahl der Zufallseffekte im Modell |
Besondere Formen des gemischten Modells
Bei Stabilitätsuntersuchungen werden zwei Modelle mit Charge als Zufallsfaktor angepasst. Das größte Modell enthält Zeit, den Zufallsfaktor Charge und die zufällige Wechselwirkung zwischen Zeit und Charge.
y = Xβ + Z1μ1 + Z2μ2 + ε
Das kleinere Modell enthält Zeit und den Zufallsfaktor Charge.
y = Xβ + Z1μ1 + ε
Die allgemeine Varianz-Kovarianz-Matrix des Vektors der Antwortvariablen y lautet:
V(σ2) = V(σ2, σ21, ... , σ2c) = σ2In + σ21Z1Z'1 + ... + σ2cZcZ'c
Dabei gilt Folgendes:
σ2 = (σ2, σ21, ... , σ2c)'
σ2, σ21, ... , σ2c werden als Varianzkomponenten bezeichnet.
Durch Faktorisieren ausgehend von der Varianz kann eine Darstellung von H(θ) gefunden werden, was sich in der Berechnung der Log-Likelihood von gemischten Modellen befindet.
V(σ2) = σ2H(θ) = σ2[In + θ1Z1Z'1 + ... + θcZcZ'c]
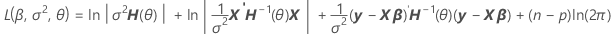
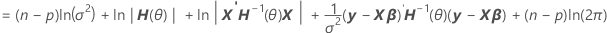
Notation
| Begriff | Beschreibung |
|---|---|
| n | Anzahl der Beobachtungen |
| p | Anzahl der Parameter in β, für Stabilitätsuntersuchungen 2 |
| σ2 | Varianzkomponente für Fehler |
| x | Designmatrix für die festen Terme, die Konstante und Zeit |
| H(θ) | In + θ1Z1Z'1 + ... + θcZcZ'c |
| In | Identitätsmatrix mit n Zeilen und Spalten |
| θi | Verhältnis der Varianz des i-ten Zufallsterm zur Fehlervarianz |
| Zi | (n x mi)-Matrix der bekannten Kodierungen für den i-ten Zufallseffekt im Modell |
| mi | Anzahl der Stufen für den i-ten Zufallseffekt |
| c | Anzahl der Zufallseffekte im Modell |
| |H(θ)| | Determinante von H(θ) |
| X' | Transposition von X |
| H–1(θ) | Inverse von H(θ) |
Box-Cox-Transformation
Bei der Box-Cox-Transformation werden Lambda-Werte (siehe unten) ausgewählt, die die Summe der Quadrate der Residuen minimieren. Die resultierende Transformation ist Y λ, wenn λ ≠ 0, und ln(Y), wenn λ = 0. Wenn λ < 0, multipliziert Minitab zudem die transformierte Antwortvariable mit −1, um die Reihenfolge aus der nicht transformierten Antwortvariablen beizubehalten.
Minitab sucht einen optimalen Wert zwischen −2 und 2. Werte, die außerhalb dieses Intervalls liegen, führen möglicherweise nicht zu einer besseren Anpassung.
Hier finden Sie einige der gängigsten Transformationen, wobei Y′ das transformierte Y der Daten darstellt:
| Lambda-Wert (λ) | Transformation |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0,5 | Y′ = 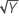 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0,5 |  |
| λ = −1 | Y′ = −1 / Y |
Modellauswahl bei Charge als Zufallsfaktor
- Zeit + Charge + Charge*Zeit (ungleiche Steigungen und Schnittpunkte mit der y-Achse bei den Chargen)
- Zeit + Charge (gleiche Steigungen und ungleiche Schnittpunkte mit der y-Achse bei den Chargen)
- Zeit (gleiche Steigungen und Schnittpunkte mit der y-Achse bei den Chargen)
Wenn die Wechselwirkung Charge*Zeit signifikant ist, wird in der Analyse das erste Modell angepasst. Wenn die Wechselwirkung nicht signifikant ist, aber der Chargenterm im zweiten Modell signifikant ist, wird in der Analyse das zweite Modell angepasst. Anderenfalls wird in der Analyse das dritte Modell angepasst.
Der Test darauf, ob Chargen zusammengefasst werden sollten, unterscheidet sich leicht vom Test darauf, ob die Charge als Faktor eingebunden werden soll, obwohl beide auf der Chi-Quadrat-Verteilung beruhen. Die Formeln für die Teststatistiken und p-Werte lauten wie folgt.
Test zwischen Modell 1 und Modell 2
Differenz = −2L2 − (−2L1)
p = 0,5 * Wahrsch(χ21 > Differenz) + 0,5 * Wahrsch(χ22 > Differenz)
Test zwischen Modell 2 und Modell 3
Differenz = −2L3 − (−2L2)
p = 0,5 * Wahrsch(χ21 > Differenz)
Notation
| Begriff | Beschreibung |
|---|---|
| La | Log-Likelihood für Modell a |
| p | p-Wert für den Test |
| Wahrsch(χ21> Differenz) | Wahrscheinlichkeit, dass eine Zufallsvariable aus einer Chi-Quadrat-Verteilung mit 1 Freiheitsgrad größer ist die Differenz ist |
| Wahrsch(χ22> Differenz) | Wahrscheinlichkeit, dass eine Zufallsvariable aus einer Chi-Quadrat-Verteilung mit 2 Freiheitsgraden größer als die Differenz ist |
Literaturhinweise
- Searle, S. R., Casella, G. und McCuloch, C. E. (1992). Variance Components
- West, B. T., Welch, K. B. und Galecki, A. T. (2007). Linear Mixed Models: A Practical Guide Using Statistical Software.
- Chow, S. (2007). Statistical Design and Analysis of Stability Studies.
