In diesem Thema
Box-Cox-Transformation
Bei der Box-Cox-Transformation werden Lambda-Werte (siehe unten) ausgewählt, die die Summe der Quadrate der Residuen minimieren. Die resultierende Transformation ist Y λ, wenn λ ≠ 0, und ln(Y), wenn λ = 0. Wenn λ < 0, multipliziert Minitab zudem die transformierte Antwortvariable mit −1, um die Reihenfolge aus der nicht transformierten Antwortvariablen beizubehalten.
Minitab sucht einen optimalen Wert zwischen −2 und 2. Werte, die außerhalb dieses Intervalls liegen, führen möglicherweise nicht zu einer besseren Anpassung.
Hier finden Sie einige der gängigsten Transformationen, wobei Y′ das transformierte Y der Daten darstellt:
| Lambda-Wert (λ) | Transformation |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0,5 | Y′ = 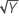 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0,5 |  |
| λ = −1 | Y′ = −1 / Y |
Modellauswahl bei fester Charge
- Zeit + Charge + Charge*Zeit (ungleiche Steigungen und Schnittpunkte mit der y-Achse bei den Chargen)
- Zeit + Charge (gleiche Steigungen und ungleiche Schnittpunkte mit der y-Achse bei den Chargen)
- Zeit (gleiche Steigungen und Schnittpunkte mit der y-Achse bei den Chargen)
Wenn die Wechselwirkung Charge*Zeit signifikant ist, wird in der Analyse das erste Modell angepasst. Wenn die Wechselwirkung nicht signifikant ist, aber der Chargenterm im zweiten Modell signifikant ist, wird in der Analyse das zweite Modell angepasst. Anderenfalls wird in der Analyse das dritte Modell angepasst.
Die Teststatistik lautet:
- Freiheitsgrade des Zählers = Freiheitsgrade für den Term
- Freiheitsgrade des Nenners = Freiheitsgrade für Fehler

Notation
| Begriff | Beschreibung |
|---|---|
| MS | Mittel der Quadrate |
| MSE | mittleres Fehlerquadrat |
| F(x) | kumulative Verteilungsfunktion der gegebenen F-Verteilung, geschätzt bei x |
Literaturhinweise
1. Chow, S. (2007). Statistical Design and Analysis of Stability Studies.
2. U.S. Department of Health and Human Services, Food and Drug Administration, (2004). Guidance for Industry, Q1E Evaluation of Stability Data.
