In diesem Thema
Angepasster Wert
Der prognostizierte y-Wert oder 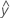 ; der Mittelwert der Antwortvariablen für die gegebenen Prädiktorwerte unter Verwendung der geschätzten Regressionsgleichung.
; der Mittelwert der Antwortvariablen für die gegebenen Prädiktorwerte unter Verwendung der geschätzten Regressionsgleichung.
Standardfehler des angepassten Randwerts (SE Anpassung)
Der Standardfehler der angepassten Randwerte im gemischten Modell hängt von der Testmethode für die festen Effekte ab. Für beide Methoden entsprechen die Standardfehler den Quadratwurzeln der Diagonalelemente der Varianzmatrix der Anpassungen.
Kenward-Roger-Methode

Dabei gilt Folgendes:
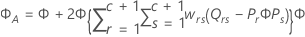
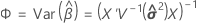
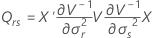
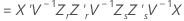
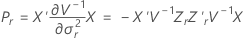
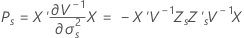
Satterthwaite-Approximation

Dabei gilt Folgendes:
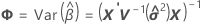
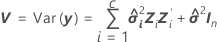
Residuen
Ein Residuum ist die Differenz zwischen einem beobachteten Wert und einem angepassten Wert. Dieser Teil der Beobachtung wird durch das angepasste Modell nicht erklärt. Das Residuum einer Beobachtung wird wie folgt ausgedrückt:
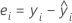
Wenn Charge ein Zufallsfaktor ist, berechnet Minitab 2 Typen von Residuen. Bei DEN Randresiduen wird der angepasste Wert für eine Zufallscharge verwendet, und daher ist der Koeffizient für die Charge nicht in der Gleichung enthalten.
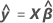
Bei den bedingten Residuen wird der angepasste Wert für eine in den Daten enthaltene Charge verwendet.
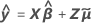
Notation
| Begriff | Beschreibung |
|---|---|
| yi | i-ter beobachteter Wert der Antwortvariablen |
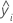 | i-ter angepasster Wert der Antwortvariablen |
 | Vektor der angepassten Werte der Antwortvariablen |
| X | Designmatrix für die festen Effekte |
 | Vektor der festen Prädiktoren |
| Z | Designmatrix für die Zufallsfaktoren |
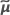 | Vektor der geschätzten BLUP-Werte |
Standardisierte Residuen

wobei die Standardabweichung des Residuums der entsprechenden diagonalen Quadratwurzel der Varianzmatrix der Residuen entspricht:
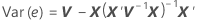
Dabei gilt Folgendes:
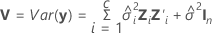
Notation
| Begriff | Beschreibung |
|---|---|
| ei | i-tes Residuum |
| Std(ei) | Standardabweichung des i-ten Residuums |
Konfidenzintervall
Der Bereich, in dem der geschätzte Mittelwert der Antwortvariablen bei einer gegebenen Gruppe von Werten der Prädiktorvariablen erwartet wird.


Dabei gilt Folgendes:
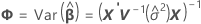
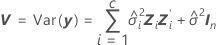
Wenn Charge ein Zufallsfaktor ist, wird für die Freiheitsgrade die folgende Formel verwendet:
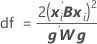
Dabei gilt Folgendes:

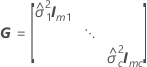
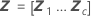
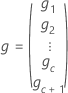

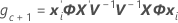
Notation
| Begriff | Beschreibung |
|---|---|
| t1-α/2, df | (1–α/2)-Quantil aus der t-Verteilung mit den angegebenen Freiheitsgraden |
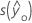 | Standardfehler des angepassten Werts |
| X | Designmatrix einschließlich der Konstanten |
| X' | Transposition von X |
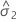 | Varianzkomponente für Fehler |
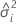 | Varianzkomponente des i-ten Zufallsfaktors |
| Zi | (n x mi)-Matrix der bekannten Kodierungen für den i-ten Zufallseffekt im Modell |
| Zi' | Transposition von Zi |
| In | Identitätsmatrix mit n Zeilen und Spalten |
| xi | Prädiktorwerte für die Anpassung oder Prognose |
| W | asymptotische Varianz-Kovarianz-Matrix der Varianzkomponente für Fehler |
| c | Anzahl der Zufallseffekte im Modell |
Prognoseintervall
Der Bereich, in dem der prognostizierte Wert der Antwortvariablen für eine neue Beobachtung erwartet wird. Die Berechnung des Prognoseintervalls hängt davon ab, ob Sie das Intervall für die Randanpassung oder die bedingte Anpassung berechnen.
Randanpassung

Dabei gilt Folgendes:
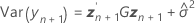

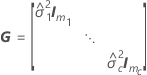
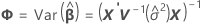
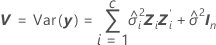
Die Freiheitsgrade für die t-Statistik werden mit der folgenden Formel angegeben:
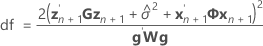
Dabei gilt Folgendes:
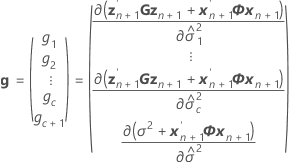


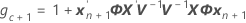
Bedingte Anpassung

Dabei gilt Folgendes:
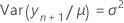
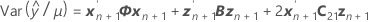
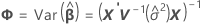
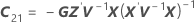
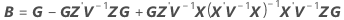
Die Freiheitsgrade für die t-Statistik entsprechen:
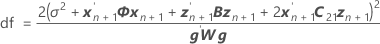
Dabei gilt Folgendes:
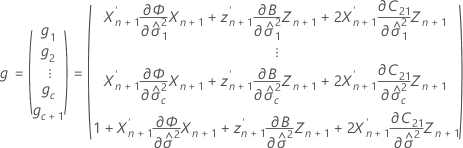

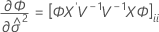
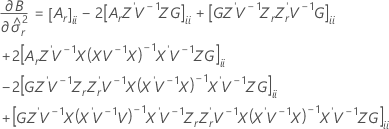
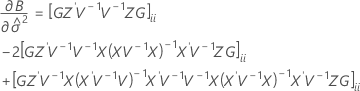
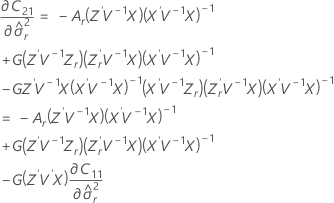
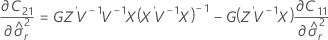
Notation
| Begriff | Beschreibung |
|---|---|
 | (1–α/2)-Quantil aus der t-Verteilung mit den angegebenen Freiheitsgraden |
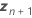 | Vektor der neuen Werte der Zufallsprädiktoren |
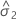 | Varianzkomponente für Fehler |
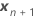 | Vektor der neuen Werte der festen Prädiktoren |
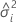 | Varianzkomponente des ii-ten Zufallsfaktors |
| Im | Identitätsmatrix mit m Zeilen und Spalten |
| m | Anzahl der Spalten in der Designmatrix, die den i-ten Zufallsterm im Modell darstellen |
| c | Anzahl der Zufallseffekte im Modell |
| Zi | (n x mi)-Designmatrix für den i-ten Zufallseffekt im Modell |
| Z'i | Transposition von Zi |
