Wählen Sie die gewünschte Methode oder Formel aus.
In diesem Thema
Koeffizient (Koef)
Ausgedrückt unter Verwendung von Matrizen lautet die Formel zum Berechnen des Vektors von Koeffizienten im Modell wie folgt:

Notation
| Begriff | Beschreibung |
|---|---|
| X | Versuchsplanmatrix |
| Y | Vektor der Antwortvariablen |
Standardfehler des Koeffizienten (SE Koef)
Die Standardfehler der Koeffizienten für die multiple Regression entsprechen den Quadratwurzeln der Diagonalelemente dieser Matrix:
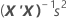
Notation
| Begriff | Beschreibung |
|---|---|
| X | Designmatrix |
| X' | transponierte Designmatrix |
| s2 | mittleres Fehlerquadrat |
t-Wert
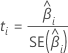
Notation
| Begriff | Beschreibung |
|---|---|
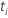 | Teststatistik für den  Koeffizienten Koeffizienten |
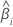 |  geschätzter Koeffizient geschätzter Koeffizient |
 | Standardfehler des  geschätzten Koeffizienten geschätzten Koeffizienten |
p-Wert – Koeffiziententabelle
Der beidseitige p-Wert für die Nullhypothese, dass ein Regressionskoeffizient gleich 0 ist, wird wie folgt ausgedrückt:
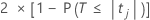
Die Freiheitsgrade sind die Freiheitsgrade für Fehler und werden wie folgt ausgedrückt:
n – p – 1
Notation
| Begriff | Beschreibung |
|---|---|
 | Kumulative Verteilungsfunktion der t-Verteilung mit Freiheitsgraden, die den Freiheitsgraden für Fehler entsprechen |
| tj | t-Statistik für den j-ten Koeffizienten |
| n | Anzahl der Beobachtungen im Datensatz |
| p | Die Summe der Freiheitsgrade für die Terme. Die Konstante zählt nicht zu den Termen. |
