In diesem Thema
Koeffizienten in gemischten Modellen
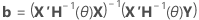
Notation
| Begriff | Beschreibung |
|---|---|
| X | Designmatrix einschließlich der Konstanten |
| X' | Transposition von X |
| Y | Daten der Antwortvariablen |
 | Inverse von  |
 |
   |
 | Identitätsmatrix mit n Zeilen und Spalten |
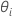 | Varianzverhältnis für den i-ten Zufallseffekt im Modell |
 | (n x mi)-Matrix der bekannten Kodierungen für den i-ten Zufallseffekt im Modell |
| mi | Anzahl der Stufen für den i-ten Zufallseffekt |
| c | Anzahl der Zufallseffekte im Modell c = 2 für das Modell mit Zeit, Charge und der Wechselwirkung Zeit*Charge c = 1 für das Modell mit Zeit und Charge |
Standardfehler der Koeffizienten in gemischten Modellen
Die Standardfehler der Koeffizienten hängen von der Testmethode für die festen Effekte ab. Weitere Einzelheiten zur Notation finden Sie im Abschnitt „Methoden“ sowie im Abschnitt „Tests von festen Effekten“.
Kenward-Roger-Approximation
Die Standardfehler der Koeffizienten sind die Quadratwurzeln der Diagonalelemente der Matrix 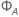 .
.
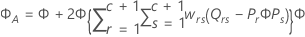
Dabei gilt Folgendes:

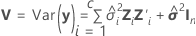
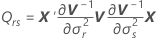
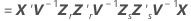
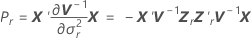
Satterthwaite-Approximation
 .
.

Dabei gilt Folgendes:
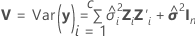
Freiheitsgrade für Koeffizienten
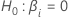
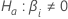
 Koeffizienten:
Koeffizienten:


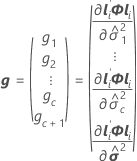

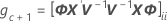
Weitere Einzelheiten zur Notation finden Sie im Abschnitt „Methoden“ sowie im Abschnitt „Tests von festen Effekten“.
Konfidenzintervalle für Koeffizienten
 Koeffizienten gilt die folgende Gleichung:
Koeffizienten gilt die folgende Gleichung:

Notation
| Begriff | Beschreibung |
|---|---|
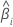 | geschätzter Koeffizient |
 | 1 − α/2-Perzentil aus der t-Verteilung mit df Freiheitsgraden |
 | Standardfehler des geschätzten Koeffizienten |
t-Wert
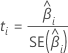
Notation
| Begriff | Beschreibung |
|---|---|
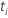 | Teststatistik für den  Koeffizienten Koeffizienten |
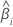 |  geschätzter Koeffizient geschätzter Koeffizient |
 | Standardfehler des  geschätzten Koeffizienten geschätzten Koeffizienten |
p-Wert (p)
Die folgende Gleichung liefert den beidseitigen p-Wert für die Nullhypothese, die besagt, dass ein Koeffizient gleich 0 ist:

Notation
| Begriff | Beschreibung |
|---|---|
 | Die Wahrscheinlichkeit, dass t entsprechend der Annahme der Nullhypothese kleiner ist als der Absolutwert des berechneten 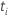 . In diesem Fall folgt t einer t-Verteilung mit df Freiheitsgraden. . In diesem Fall folgt t einer t-Verteilung mit df Freiheitsgraden. |
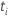 | Der t-Wert für den  Koeffizienten. Koeffizienten. |
