Summe der Quadrate (SS)
In Bezug auf Matrizen lauten die Formeln für die verschiedenen Summen der Quadrate wie folgt:

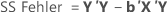
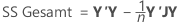
Minitab schlüsselt die Komponenten der Summe der Quadrate der Regression bzw. der Behandlungen in den Teil der Streuung auf, der durch die einzelnen Terme erklärt wird, wobei sowohl die sequenzielle Summe der Quadrate als auch die korrigierte Summe der Quadrate verwendet werden.
Notation
| Begriff | Beschreibung |
|---|---|
| b | Vektor von Koeffizienten |
| X | Designmatrix |
| Y | Vektor von Werten der Antwortvariablen |
| n | Anzahl der Beobachtungen |
| J | (n x n)-Matrix von 1s |
Kor MS – Regression
Die Formel für das Mittel der Quadrate (MS) der Regression lautet wie folgt:
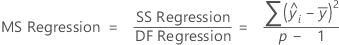
Notation
| Begriff | Beschreibung |
|---|---|
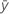 | Mittelwert der Antwortvariablen |
 | i-ter angepasster Wert der Antwortvariablen |
| p | Anzahl der Terme im Modell |
Kor MS – Fehler
Das mittlere Fehlerquadrat (das auch als MS Fehler oder MSE abgekürzt und als s2 angegeben wird) ist die Varianz um die angepasste Regressionslinie. Die Formel lautet wie folgt:

Notation
| Begriff | Beschreibung |
|---|---|
| yi | i-ter beobachteter Wert der Antwortvariablen |
 | i-ter angepasster Wert der Antwortvariablen |
| n | Anzahl der Beobachtungen |
| p | Anzahl der Koeffizienten im Modell, wobei die Konstante nicht gezählt wird |
F
Wenn alle Faktoren im Modell fest sind, hängt die Berechnung der F-Statistik wie folgt vom Gegenstand des Hypothesentests ab:
- F(Term)
-

- F(fehlende Anpassung)
-

Wenn Zufallsfaktoren im Modell enthalten sind, wird F mit dem erwarteten Mittel der Quadrate für jeden Term bestimmt. Weitere Informationen finden Sie in Neter et al.1.
Notation
| Begriff | Beschreibung |
|---|---|
| Kor MS Term | Ein Maß der Streuung, die durch einen Term erklärt wird, nachdem die anderen Terme im Modell berücksichtigt wurden. |
| MS Fehler | Ein Maß der Streuung, die durch das Modell nicht erklärt wird. |
| MS Fehlende Anpassung | Ein Maß der Streuung in der Antwortvariablen, die durch Hinzufügen weiterer Terme zum Modell modelliert werden könnte. |
| MS Reiner Fehler | Ein Maß der Streuung in replizierten Antwortdaten. |
- J. Neter, W. Wasserman und M. H. Kutner (1985). Applied Linear Statistical Models, Second Edition. Irwin, Inc.
p-Wert (p)
p-Werte werden in Hypothesentests verwendet, um Ihnen die Entscheidung zu ermöglichen, ob eine Nullhypothese zurückgewiesen oder nicht zurückgewiesen werden sollte. Der p-Wert stellt die Wahrscheinlichkeit dar, eine Teststatistik zu erhalten, die mindestens so extrem wie der tatsächlich berechnete Wert ist, wenn die Nullhypothese wahr ist. Ein häufig verwendeter Trennwert für den p-Wert ist 0,05. Wenn beispielsweise der berechnete p-Wert einer Teststatistik kleiner als 0,05 ist, weisen Sie die Nullhypothese zurück.
