In diesem Thema
- Schritt 1: Bestimmen, ob die Assoziation zwischen der Antwortvariablen und dem Term statistisch signifikant ist
- Schritt 2: Bestimmen der Haltbarkeit des Produkts
- Schritt 3: Untersuchen der Assoziation zwischen Term und Antwortvariable
- Schritt 4: Bestimmen, wie gut das Modell an die Daten angepasst ist
- Schritt 5: Bestimmen, ob das Modell die Annahmen der Analyse erfüllt
Schritt 1: Bestimmen, ob die Assoziation zwischen der Antwortvariablen und dem Term statistisch signifikant ist
Wenn Ihre Daten einen Chargenfaktor enthalten, werden in der Tabelle der Modellauswahl die Ergebnisse des Modellauswahlprozesses angezeigt. Minitab schätzt die Haltbarkeit anhand des endgültigen Modells aus dem Auswahlprozess.
Minitab beginnt mit dem vollständigen Modell, das Zeit, Charge und die Wechselwirkung Charge*Zeit umfasst. Anschließend vergleicht Minitab den p-Wert für die Wechselwirkung mit dem im Feld Alpha zum Zusammenfassen von Chargen angegebenen Wert (auch als α bezeichnet). Wenn der p-Wert für die Wechselwirkung kleiner als α ist, kann das Modell nicht reduziert werden. Das endgültige Modell enthält alle drei Terme.
Wenn der p-Wert für die Wechselwirkung größer oder gleich α ist, entfernt Minitab die Wechselwirkung und wertet das reduzierte Modell aus, das nur die Zeit und die Charge umfasst. Wenn der p-Wert für die Charge im reduzierten Modell kleiner als α ist, kann das Modell nicht weiter reduziert werden. Das endgültige Modell enthält die Zeit und die Charge.
Wenn der p-Wert für Charge im reduzierten Modell größer oder gleich α ist, entfernt Minitab die Charge. Das endgültige Modell enthält nur noch die Zeit.
Modellauswahl mit α = 0,25
| Quelle | DF | Seq SS | Seq MS | F-Wert | p-Wert |
|---|---|---|---|---|---|
| Monat | 1 | 122,460 | 122,460 | 345,93 | 0,000 |
| Charge | 4 | 2,587 | 0,647 | 1,83 | 0,150 |
| Monat*Charge | 4 | 3,850 | 0,962 | 2,72 | 0,048 |
| Fehler | 30 | 10,620 | 0,354 | ||
| Gesamt | 39 | 139,516 |
Wichtigste Ergebnisse: p-Wert
In diesem Beispiel, in dem die Charge ein fester Faktor ist, beträgt der p-Wert für die Wechselwirkung Monat*Charge 0,048. Da der p-Wert kleiner als das Signifikanzniveau 0,25 ist, sind die Steigungen für die einzelnen Chargen in den Regressionsgleichungen unterschiedlich.
Schritt 2: Bestimmen der Haltbarkeit des Produkts
In der Tabelle „Schätzung der Haltbarkeit“ werden die Spezifikationsgrenzen, das für die Berechnung der Haltbarkeit verwendete Konfidenzniveau und die Schätzungen der Haltbarkeit angezeigt.
Wenn Charge ein fester Faktor und im endgültigen Modell nicht enthalten ist, ist die Haltbarkeit für alle Chargen gleich. Anderenfalls ist die Haltbarkeit für jede Charge unterschiedlich, und Minitab zeigt für jede Charge eine Schätzung der Haltbarkeit an. Die Gesamthaltbarkeit des Produkts entspricht dem kleinsten individuellen Haltbarkeitswert.
Wenn Charge ein Zufallsfaktor ist, berechnet Minitab nur die Gesamthaltbarkeit.
Schätzung der Haltbarkeit
Haltbarkeit = Zeitraum, während dessen Sie zu 95 % sicher sein können, dass mindestens 50 %
der Antwortwerte über der unteren Spezifikationsgrenze liegen
| Charge | Haltbarkeit |
|---|---|
| 1 | 83,552 |
| 2 | 54,790 |
| 3 | 57,492 |
| 4 | 60,898 |
| 5 | 66,854 |
| Gesamt | 54,790 |
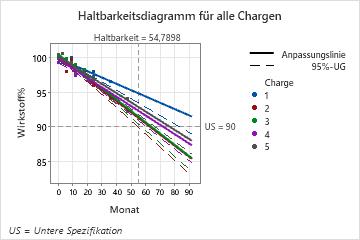
Wichtigste Ergebnisse: Schätzungen der Haltbarkeit, Haltbarkeitsdiagramm
In diesen Ergebnissen enthält das endgültige Modell den Chargenfaktor, Minitab zeigt also die Schätzungen der Haltbarkeit für jede Charge an. Die Gesamthaltbarkeit beträgt 54,79 Monate. Dieser Wert entspricht der Haltbarkeit für Charge 2, die Charge mit der kürzesten Haltbarkeit.
Schritt 3: Untersuchen der Assoziation zwischen Term und Antwortvariable
Wenn bei einem festen Chargenfaktor die Zeit im endgültigen Modell der einzige Term ist, weisen alle Chargen denselben Schnittpunkt mit der y-Achse und dieselbe Steigung auf, und Minitab zeigt nur eine Regressionsgleichung an. Andernfalls zeigt Minitab für jede Charge eine separate Gleichung an. Wenn der Chargenfaktor im endgültigen Modell enthalten ist, nicht aber die Wechselwirkung Charge*Zeit, weisen alle Chargen unterschiedliche Schnittpunkte mit der y-Achse, aber dieselbe Abbaurate auf. Wenn sowohl der Chargenterm als auch die Wechselwirkung Charge*Zeit im endgültigen Modell enthalten sind, weisen alle Chargen unterschiedliche Schnittpunkte mit der y-Achse und Steigungen auf.
Regressionsgleichung
| Charge | |||
|---|---|---|---|
| 1 | Wirkstoff% | = | 99,853 - 0,0909 Monat |
| 2 | Wirkstoff% | = | 100,153 - 0,1605 Monat |
| 3 | Wirkstoff% | = | 100,479 - 0,1630 Monat |
| 4 | Wirkstoff% | = | 99,769 - 0,1350 Monat |
| 5 | Wirkstoff% | = | 100,173 - 0,1323 Monat |
Wichtigste Ergebnisse: Regressionsgleichung
In diesen Ergebnissen sind sowohl Monat als auch die Wechselwirkung Monat*Charge signifikant. Die Regressionsgleichungen für die einzelnen Chargen weisen daher unterschiedliche Schnittpunkte mit der y-Achse und Steigungen auf. Charge 3 weist die steilste Steigung auf (−0,1630), was darauf hinweist, dass die Konzentration des Medikaments (Wirkstoff%) für Charge 3 jeden Monat um 0,163 Prozentpunkte abnimmt. Charge 4 weist den kleinsten Schnittpunkt mit der y-Achse auf (99,769), was darauf hinweist, dass bei Charge 4 zum Zeitpunkt null die Konzentration am geringsten war.
Schritt 4: Bestimmen, wie gut das Modell an die Daten angepasst ist
Um zu ermitteln, wie gut das Modell an die Daten angepasst ist, untersuchen Sie die Statistiken für die Güte der Anpassung in der Tabelle „Zusammenfassung des Modells“.
- R-Qd
-
R2 gibt den Prozentsatz der Streuung der Antwortvariablen an, der durch das Modell erklärt wird. Je höher das R2, desto besser ist das Modell an die Daten angepasst. Das R2 liegt immer zwischen 0 % und 100 %.
Der Wert von R2 nimmt beim Einbinden zusätzlicher Prädiktoren in das Modell stets zu. Das beste Modell mit fünf Prädiktoren weist beispielsweise immer ein R2 auf, das mindestens so hoch wie das des besten Modells mit vier Prädiktoren ist. Daher ist R2 am nützlichsten, wenn Sie Modelle derselben Größe vergleichen.
- R-Qd (kor)
-
Verwenden Sie das korrigierte R2, wenn Sie Modelle vergleichen möchten, die eine unterschiedliche Anzahl von Prädiktoren enthalten. R2 nimmt stets zu, wenn Sie einen zusätzlichen Prädiktor in das Modell aufnehmen, selbst wenn damit keine tatsächliche Verbesserung des Modells verbunden ist. Der Wert des korrigierten R2 berücksichtigt die Anzahl der Prädiktoren im Modell, so dass Ihnen das Auswählen des richtigen Modells erleichtert wird.
-
Kleine Stichproben ermöglichen keinen genauen Schätzwert für die Stärke der Beziehung zwischen der Antwortvariablen und den Prädiktoren. Wenn z. B. das R2 genauer sein muss, sollten Sie einen größeren Stichprobenumfang (im Allgemeinen 40 oder mehr) wählen.
-
Statistiken für die Güte der Anpassung sind nur eines der Maße für die Güte der Anpassung des Modells an die Daten. Selbst wenn ein Modell einen erwünschten Wert aufweist, sollten Sie die Residuendiagramme untersuchen, um sich zu vergewissern, dass das Modell die Modellannahmen erfüllt.
Zusammenfassung des Modells
| S | R-Qd | R-Qd(kor) | R-Qd(prog) |
|---|---|---|---|
| 0,594983 | 92,39% | 90,10% | 85,22% |
Wichtigste Ergebnisse: R-sq
In diesen Ergebnissen liegen sowohl das R2 als auch das angepasste R2 nahe bei 100, was darauf hinweist, dass das Modell gut an die Daten angepasst ist.
Schritt 5: Bestimmen, ob das Modell die Annahmen der Analyse erfüllt
Verwenden Sie die Residuendiagramme, um zu ermitteln, ob das Modell angemessen ist und die Annahmen der Analyse erfüllt. Wenn die Annahmen nicht erfüllt werden, ist das Modell u. U. nicht gut an die Daten angepasst, und Sie sollten beim Interpretieren der Ergebnisse vorsichtig sein.
Hinweis
Wenn das Modell Charge als Zufallsfaktor enthält, können Sie die Randresiduen und die bedingten Residuen grafisch darstellen. Die Randanpassungen sind die angepassten Werte für die Grundgesamtheit. Verwenden Sie die bedingten Residuen, um zu prüfen, ob der Fehlerterm im Modell normalverteilt ist.
Diagramm der Residuen im Vergleich zu den Anpassungen
Verwenden Sie das Diagramm der Residuen im Vergleich zu den Anpassungen, um die Annahme zu überprüfen, dass die Residuen zufällig verteilt sind und eine konstante Varianz aufweisen. Im Idealfall sollten die Punkte zufällig auf beiden Seiten von null verteilt sein, und es sollten keine Muster in den Punkten erkennbar sein.
| Muster | Mögliche Bedeutung des Musters |
|---|---|
| Aufgefächerte oder ungleichmäßig gestreute Residuen für die angepassten Werte | Nicht konstante Varianz |
| Krümmung | Ein fehlender Term höherer Ordnung |
| Ein weit von null entfernt liegender Punkt | Ein Ausreißer |
| Ein in x-Richtung weit von den anderen Punkten entfernter Punkt | Ein einflussreicher Punkt |
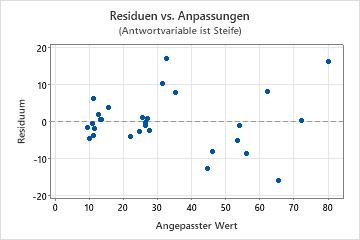
Diagramm der Residuen im Vergleich zur Reihenfolge
Trend
Shift
Zyklus
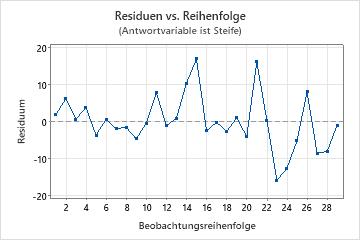
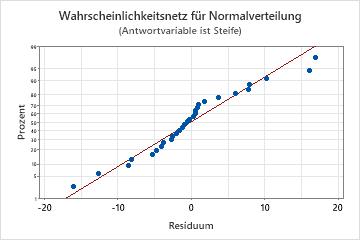
Wahrscheinlichkeitsnetz für Normalverteilung
Verwenden Sie das Wahrscheinlichkeitsnetz (Normal) der Residuen, um die Annahme zu überprüfen, dass die Residuen normalverteilt sind. Die Residuen im Wahrscheinlichkeitsnetz für Normalverteilung sollten ungefähr einer Geraden folgen.
| Muster | Mögliche Bedeutung des Musters |
|---|---|
| Keine Gerade | Nicht-Normalverteilung |
| Ein Punkt weit entfernt von der Linie | Ein Ausreißer |
| Unbeständige Steigung | Eine nicht identifizierte Variable |
Weitere Informationen zum Umgang mit Mustern in den Residuendiagrammen finden Sie unter Residuendiagramme für Darstellung der Anpassungslinie.
