In diesem Thema
Histogramm der Residuen
Im Histogramm der Residuen wird die Verteilung der Residuen für alle Beobachtungen veranschaulicht.
Interpretation
| Muster | Mögliche Bedeutung des Musters |
|---|---|
| Ein langer Randbereich in einer Richtung | Schiefe |
| Ein Balken weit entfernt von den anderen Balken | Ein Ausreißer |
Da die Darstellung eines Histogramms von der Anzahl der Intervalle abhängt, mit denen die Daten gruppiert werden, verwenden Sie ein Histogramm nicht, um die Normalverteilung der Residuen zu beurteilen. Verwenden Sie dazu stattdessen ein Wahrscheinlichkeitsnetz für Normalverteilung.
Ein Histogramm ist am effektivsten, wenn Sie über mindestens ca. 20 Datenpunkte verfügen. Wenn die Stichprobe zu klein ist, enthalten die einzelnen Balken im Histogramm keine ausreichende Menge an Datenpunkten, um Schiefe und Ausreißer zuverlässig darzustellen.
Wahrscheinlichkeitsnetz (Normal) für Residuen
Das Wahrscheinlichkeitsnetz (Normal) für Residuen stellt die Residuen im Vergleich zu den Werten dar, die bei Vorliegen einer Normalverteilung erwartet würden.
Hinweis
Wenn Charge ein Zufallsfaktor ist, verwenden Sie die bedingten Residuen, um zu prüfen, ob eine Normalverteilung vorliegt.
Interpretation
Verwenden Sie das Wahrscheinlichkeitsnetz (Normal) der Residuen, um die Annahme zu überprüfen, dass die Residuen normalverteilt sind. Die Residuen im Wahrscheinlichkeitsnetz für Normalverteilung sollten ungefähr einer Geraden folgen.
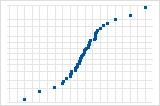
Die S-Kurve deutet auf eine Verteilung mit langen Randbereichen hin.
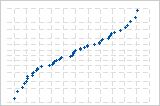
Die invertierte S-Kurve deutet auf eine Verteilung mit kurzen Randbereichen hin.
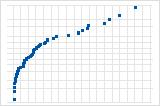
Eine Abwärtskurve deutet auf eine rechtsschiefe Verteilung hin.
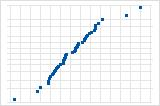
Wenige Punkte, die abseits der Linie liegen, deuten auf eine Verteilung mit Ausreißern hin.
Wenn Sie ein nicht normalverteiltes Muster feststellen, prüfen Sie das Modell anhand der übrigen Residuendiagramme auf andere Probleme, z. B. auf nicht konstante Varianz oder einen Effekt der chronologischen Reihenfolge. Wenn die Residuen keiner Normalverteilung folgen und die Daten weniger als 15 Beobachtungen umfassen, sind die Konfidenzintervalle für die Prognosen, die Konfidenzintervalle für die Koeffizienten und die p-Werte für die Koeffizienten möglicherweise ungenau.
Residuen vs. Anpassungen

Diagramm mit Ausreißer
Einer der Punkte ist viel größer als alle anderen Punkte. Daher handelt es sich bei dem Punkt um einen Ausreißer. Wenn zu viele Ausreißer auftreten, ist das Modell möglicherweise nicht akzeptabel. Versuchen Sie nach Möglichkeit, die Ursache von Ausreißern zu ermitteln. Korrigieren Sie sämtliche Dateneingabe- oder Messfehler. Erwägen Sie, Datenwerte zu entfernen, die auf ungewöhnliche, einmalige Ereignisse (Ausnahmebedingungen) zurückzuführen sind. Wiederholen Sie anschließend die Analyse.
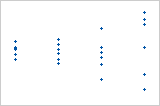
Diagramm mit nicht konstanter Varianz
Die Varianz der Residuen nimmt mit den angepassten Werten zu. Beachten Sie, dass sich bei zunehmenden Werten der Anpassungen die Streuung der Residuen verbreitert. Dieses Muster weist darauf hin, dass die Varianzen der Residuen ungleich (nicht konstant) sind.
Wenn Sie Muster oder Ausreißer in einem Diagramm der Residuen im Vergleich zu den Anpassungen feststellen, erwägen Sie die folgenden Lösungen:
| Problem | Mögliche Lösung |
|---|---|
| Nicht konstante Varianz | Erwägen Sie, eine Box-Cox-Transformation zu verwenden. Weitere Informationen finden Sie unter Durchführen einer Box-Cox-Transformation für Stabilitätsuntersuchung. |
| Ein Ausreißer oder ein einflussreicher Punkt |
|
Residuen vs. Reihenfolge
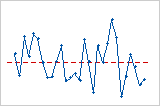
Das Diagramm der Residuen im Vergleich zur Reihenfolge zeigt die Residuen in der Reihenfolge an, in der die Daten erfasst wurden.
Interpretation
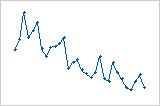
Trend
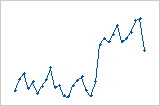
Shift
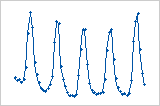
Zyklus
Residuen vs. Variablen
Das Diagramm der Residuen vs. Variablen zeigt die Residuen im Vergleich mit einer anderen Variablen. Die Variable kann bereits im Modell enthalten sein. Es ist auch möglich, dass die Variable nicht im Modell enthalten ist, und Sie vermuten, dass sie die Antwortvariable beeinflusst.
Interpretation
Wenn Sie ein nicht zufälliges Muster in den Residuen feststellen, weist dies darauf hin, dass sich die Variable systematisch auf die Antwortvariable auswirkt. Erwägen Sie, diese Variable in eine Analyse einzubinden.
