In diesem Thema
Regressionsgleichung
Verwenden Sie die Regressionsgleichung, um die Beziehung zwischen der Antwortvariablen und den Termen im Modell zu beschreiben. Die Regressionsgleichung ist eine algebraische Darstellung der Regressionslinie. Die Regressionsgleichung für das lineare Modell nimmt die folgende Form an: Y = b0 + b1x1. In der Regressionsgleichung steht Y für die Antwortvariable, b0 ist die Konstante bzw. der Schnittpunkt mit der y-Achse, b1 ist der geschätzte Koeffizient für den linearen Term (auch als Steigung der Linie bezeichnet), und x1 steht für den Wert des Terms.
Die Regressionsgleichung mit mehreren Termen weist die folgende Form auf:
y = b0 + b1x1 + b2x2 + ... + bkxk
- y ist die Antwortvariable.
- b0 ist die Konstante.
- b1, b2, ..., bk sind die Koeffizienten.
- x1, x2, ..., xk sind die Werte des Terms.
Wenn das Modell sowohl stetige als auch kategoriale Variablen enthält, wird in der Tabelle der Regressionsgleichung möglicherweise eine Gleichung für jede Kombination von Stufen der kategorialen Variablen angezeigt. Um diese Gleichungen für die Prognose zu verwenden, müssen Sie entsprechend den Werten der kategorialen Variablen die richtige Gleichung auswählen und anschließend die Werte der stetigen Variablen einsetzen.
Variableneinstellungen
Das Modell verwendet die Einstellungen für die Variablen zum Berechnen der Prognosen. Wenn die Variableneinstellungen im Vergleich zu den Daten, auf deren Grundlage Minitab das Modell geschätzt hat, ungewöhnlich sind, zeigt Minitab unter der Prognose eine Warnung an.
Anpassung
Angepasste Werte sind auch bekannt als Anpassungen oder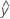 
. Die angepassten Werte sind Punktschätzungen des Mittelwerts der Antwortvariablen für die gegebenen Werte der Prädiktoren. Die Werte der Prädiktoren werden auch als x-Werte bezeichnet.
Interpretation
Angepasste Werte werden durch Einsetzen der spezifischen x-Werte für jede Beobachtung im Datensatz in die Modellgleichung berechnet.
Wenn die Gleichung beispielsweise y = 5 + 10x lautet, ergibt ein x-Wert von 2 den angepassten Wert 25 (25 = 5 + 10(2)).
Minitab kennzeichnet Prognosen, deren Prädiktorwerte im Vergleich zu den Werten in den Daten ungewöhnlich sind. Nur weitere Tests mit älteren Stichproben können bestätigen, dass Ihre Schätzwerte für die Haltbarkeit genau sind.
SE Anpassung
Der Standardfehler der Anpassung (SE Anpassung) ist ein Schätzwert der Streuung im geschätzten Mittelwert der Antwortvariablen für die angegebenen Variableneinstellungen. Der Standardfehler der Anpassung wird bei der Berechnung des Konfidenzintervalls für den Mittelwert der Antwortvariablen verwendet. Standardfehler sind immer nicht negativ.
Interpretation
Verwenden Sie den Standardfehler der Anpassung, um zu ermitteln, wie genau der Schätzwert für den Mittelwert der Antwortvariablen ist. Je kleiner der Standardfehler, desto genauer ist der prognostizierte Mittelwert der Antwortvariablen. Ein Analytiker entwickelt beispielsweise ein Modell, um die Lieferzeit zu prognostizieren. Für einen Satz von Variableneinstellungen prognostiziert das Modell eine mittlere Lieferzeit von 3,80 Tagen. Der Standardfehler der Anpassung für diese Einstellungen beträgt 0,08 Tage. Für einen zweiten Satz von Variableneinstellungen errechnet das Modell dieselbe mittlere Lieferzeit mit einem Standardfehler der Anpassung von 0,02 Tagen. Der Analytiker kann sich sicherer sein, dass die mittlere Lieferzeit für den zweiten Satz von Variableneinstellungen nahe an 3,80 Tagen liegt.
Der Standardfehler der Anpassung kann in Verbindung mit dem angepassten Wert verwendet werden, um ein Konfidenzintervall für den Mittelwert der Antwortvariablen zu erstellen. Angenommen, ein 95%-Konfidenzintervall erstreckt sich (je nach Freiheitsgraden) ungefähr +/- zwei Standardfehler um den prognostizierten Mittelwert. Für die Lieferzeiten beträgt das 95%-Konfidenzintervall des prognostizierten Mittelwerts von 3,80 Tagen bei einem Standardfehler von 0,08 (3,64; 3,96) Tage. Sie können sich zu 95 % sicher sein, dass der Mittelwert der Grundgesamtheit in diesem Bereich liegt. Wenn der Standardfehler 0,02 beträgt, ist das 95%-Konfidenzintervall (3,76; 3,84) Tage. Das Konfidenzintervall für den zweiten Satz von Variableneinstellungen ist schmaler, weil der Standardfehler kleiner ist.
Konfidenzintervall für Anpassung (95%-KI)
Diese Konfidenzintervalle (KI) sind Bereiche von Werten, die wahrscheinlich den Mittelwert der Antwortvariablen für die Grundgesamtheit enthalten, die die beobachteten Werte der Prädiktoren bzw. Faktoren im Modell aufweist.
Da die Stichproben zufällig sind, ist es unwahrscheinlich, dass zwei Stichproben aus einer Grundgesamtheit identische Konfidenzintervalle ergeben. Wenn Sie die Stichprobennahme jedoch viele Male wiederholen, enthält ein gewisser Prozentsatz der resultierenden Konfidenzintervalle den unbekannten Parameter der Grundgesamtheit. Der Prozentsatz dieser Konfidenzintervalle, die den Parameter enthalten, stellt das Konfidenzniveau des Intervalls dar.
Das Konfidenzintervall setzt sich aus den folgenden zwei Teilen zusammen:
Interpretation
Verwenden Sie das Konfidenzintervall, um den Schätzwert des angepassten Werts für die beobachteten Werte der Variablen auszuwerten.
Bei einem 95%-Konfidenzniveau können Sie sich beispielsweise zu 95 % sicher sein, dass das Konfidenzintervall den Mittelwert der Grundgesamtheit für die angegebenen Werte der Prädiktorvariablen oder Faktoren im Modell enthält. Anhand des Konfidenzintervalls können Sie die praktische Signifikanz Ihrer Ergebnisse beurteilen. Bestimmen Sie anhand Ihrer Fachkenntnisse, ob das Konfidenzintervall Werte umfasst, die in der jeweiligen Situation von praktischer Signifikanz sind. Ein breites Konfidenzintervall deutet darauf hin, dass Sie sich bezüglich des Mittelwerts von künftigen Werten weniger sicher sein können. Wenn das Intervall zu breit und damit nicht hilfreich ist, erwägen Sie, den Stichprobenumfang zu vergrößern.
95%-PI
Das Prognoseintervall ist ein Bereich, der wahrscheinlich einen einzelnen künftigen Wert der Antwortvariablen für eine ausgewählte Kombination von Variableneinstellungen enthält. Das Prognoseintervall ist immer breiter als das entsprechende Konfidenzintervall.
Interpretation
Ein Qualitätstechniker hat z. B. ermittelt, dass die Haltbarkeit eines neuen Medikaments 54,79 Monate beträgt. Die Haltbarkeit ist für diese Analyse definiert als die Zeit, nach deren Ablauf sich der Techniker nicht mehr zu 95 % sicher sein kann, dass die Konzentration der schlechtesten Charge 90 % der beabsichtigten Konzentration beträgt. Der Techniker möchte die mittlere Konzentration für die schlechteste Charge nach 54,79 Monaten prognostizieren.
In diesen Ergebnissen lautet die Prognose für den Mittelwert der Antwortvariablen ungefähr 91,36 %. Der Techniker möchte jedoch außerdem den Wertebereich für eine einzelne Tablette aus Charge 2 schätzen. Das Prognoseintervall gibt an, dass Sie sich zu 95 % sicher sein können, dass die prognostizierte Konzentration für eine einzelne Tablette aus Charge 2 nach 54,79 Monaten zwischen ungefähr 89,3217 % und 93,4001 % liegt.
Einstellungen
| Variable | Einstellung |
|---|---|
| Monat | 54,79 |
| Charge | 2 |
Prognose
| Anpassung | SE Anpassung | 95%-KI | 95%-PI | |
|---|---|---|---|---|
| 91,3609 | 0,801867 | (89,7233; 92,9986) | (89,3217; 93,4001) | XX |
