In diesem Thema
Koeffizienten und standardisierte Koeffizienten
Die Koeffizienten sind die Parameter in einer Regressionsgleichung. Die geschätzten Koeffizienten werden zusammen mit den Prädiktoren verwendet, um den angepassten Wert der Antwortvariablen und den prognostizierten Wert der Antwortvariablen für neue Beobachtungen zu berechnen. Im Gegensatz zu kleinsten Quadraten sind die PLS-Koeffizienten nichtlineare Schätzwerte. Die standardisierten Koeffizienten geben die Relevanz der einzelnen Prädiktoren im Modell an, und sie entsprechen den standardisierten x- und y-Variablen. In der PLS-Regression wird die Koeffizientenmatrix (Größe p × r) aus den Gewichtungen und Ladungen berechnet.
Die Formel für die standardisierten Koeffizienten lautet:

Zur Berechnung der nicht standardisierten Koeffizienten und des Schnittpunkts mit der y-Achse werden die folgenden Formeln verwendet:
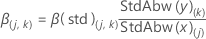

Notation
| Begriff | Beschreibung |
|---|---|
| W | Matrix der x-Gewichtungen |
| P | Matrix der x-Ladungen |
| C | Matrix der y-Ladungen |
| j | Prädiktoren (1; p) |
| k | Werte der Antwortvariablen (1; r) |
| p | Anzahl der Prädiktoren |
| r | Anzahl der Werte der Antwortvariablen |
Hebelwirkungen
Bei der Regression der kleinsten Quadrate sind Hebelwirkungen Werte, die angeben, wie weit die entsprechenden Beobachtungen von der Mitte des x-Raums entfernt liegen, der durch die x-Werte beschrieben wird. In PLS werden die Prädiktoren durch x-Werte ersetzt. Beobachtungen mit einer großen Hebelwirkung weisen weit von null entfernte x-Werte auf und beeinflussen die Regressionskoeffizienten signifikant. Punkte mit einer großen Hebelwirkung sind Ausreißer im x-Raum, aber nicht unbedingt Ausreißer im y-Raum.
Die Hebelwirkungswerte in der PLS-Regression werden anhand der Matrix T der x-Werte berechnet. Hiermit wird wie folgt die „Dach-Matrix“ (Hat-Matrix (H) berechnet:

Die Hebelwirkung (hii) der i-ten Beobachtung ist das i-te Diagonalelement der H-Matrix.
Ein Hebelwirkungswert größer als 2m/n gilt als hoch und sollte untersucht werden.
Notation
| Begriff | Beschreibung |
|---|---|
| n | Anzahl der Beobachtungen |
| m | Anzahl der Komponenten |
Distanzen vom x-Modell
Dies ist ein Maß dafür, wie gut die Anpassung an die Beobachtungen im x-Raum ist; hiermit wird angegeben, wie gut die x-Werte die Beobachtungen beschreiben. Eine Beobachtung mit einer großen Distanz kann auch ein Hebelwirkungspunkt sein.
Formel
Die Formel zum Berechnen der Distanz vom x-Modell für die i-te Beobachtung lautet wie folgt:
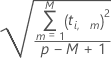
Notation
| Begriff | Beschreibung |
|---|---|
| M | Anzahl der Komponenten |
| t | x-Wert |
| p | Anzahl der Prädiktoren |
Distanzen vom y-Modell
Dies ist ein Maß dafür, wie gut die Anpassung an die Beobachtungen im y-Raum ist; hiermit wird angegeben, wie gut die y-Werte die Beobachtungen beschreiben. Eine Beobachtung mit einer großen Distanz kann auch ein Ausreißer sein.
Formel
Die Formel zum Berechnen der Distanz vom y-Modell für die i-te Beobachtung lautet wie folgt:
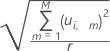
Notation
| Begriff | Beschreibung |
|---|---|
| M | Anzahl der Komponenten |
| u | y-Wert |
| r | Anzahl der Werte der Antwortvariablen |
