In diesem Thema
x-Werte
Bei den x-Werten handelt es sich um lineare Kombinationen der Terme; sie ähneln den Werten der Hauptkomponenten. Die x-Werte bilden eine n × m-Matrix nicht korrelierender Spalten. Die x-Werte stellen Projektionen der Beobachtungen auf die PLS-Komponenten dar. PLS passt die x-Werte an, die die ursprünglichen Terme in den Daten ersetzen, wobei die Schätzung kleinster Quadrate verwendet wird.
Formel
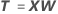
Notation
| Begriff | Beschreibung |
|---|---|
| n | Anzahl der Beobachtungen |
| m | Anzahl der Komponenten |
| i | Beobachtungen von 1 bis n |
| j | Terme von 1 bis p |
| X | Versuchsplanmatrix |
| W | Matrix der x-Gewichtungen |
x-Ladungen
Die x-Ladungen sind die linearen Koeffizienten, die die Terme mit den x-Werten verknüpfen, ähnlich den Eigenvektoren in der Hauptkomponentenanalyse. Die Werte der Ladungen geben die Relevanz des entsprechenden Terms für die m-te Komponente an. Die x-Ladungen bilden eine p × m-Matrix.
Formel
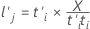
Notation
| Begriff | Beschreibung |
|---|---|
| p | Anzahl der Terme |
| m | Anzahl der Komponenten |
| i | Beobachtungen von 1 bis n |
| j | Terme von 1 bis p |
| t | x-Werte |
| X | Prädiktoren |
x-Gewichtungen
Die x-Gewichtungen beschreiben die Kovarianz zwischen den Termen und den Antwortvariablen. Im Algorithmus wird mit Hilfe der Gewichtungen sichergestellt, dass die x-Werte orthogonal sind (in keiner Beziehung zueinander stehen), und sie werden zum Berechnen der x-Werte verwendet. Die x-Gewichtungen bilden eine (p × m)-Matrix.
Formel
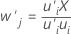
Minitab skaliert die Vektoren der Gewichtungen, so dass die Länge des Vektors 1 beträgt.
Notation
| Begriff | Beschreibung |
|---|---|
| p | Anzahl der Terme |
| m | Anzahl der Komponenten |
| i | die Beobachtungen von 1 bis n |
| j | die Terme von 1 bis p |
| X | die Matrix der x-Residuen |
| u | die y-Werte |
x-Residuen
Die x-Residuen enthalten die Streuung in den Prädiktoren, die vom PLS-Modell nicht erklärt wird. Beobachtungen mit relativ großen x-Residuen sind Ausreißer im x-Raum und werden vom Modell nicht gut erklärt.
Die x-Residuen sind die Differenzen zwischen den tatsächlichen Prädiktorwerten und den x-berechneten Werten, und sie befinden sich auf derselben Skala wie die ursprünglichen Prädiktoren. Die Matrix der x-Residuen ist, ähnlich wie die ursprüngliche x-Matrix, eine (n × p)-Matrix.
Die Matrix der x-Residuen wird anfänglich auf die Matrix der standardisierten x-Werte festgelegt. Nach der Berechnung der m-ten Komponente sowie der Vektoren der x-Werte und der x-Ladungen berechnet Minitab die x-Residuen.
Formel

Anschließend berechnet Minitab die nicht standardisierten x-Residuen, indem die standardisierten x-Residuen mit der Standardabweichung der Prädiktorwerte multipliziert werden.
Notation
| Begriff | Beschreibung |
|---|---|
| n | Anzahl der Beobachtungen |
| p | Anzahl der Terme |
| i | Beobachtungen von 1 bis n |
| j | Terme von 1 bis p |
| t | x-Werte |
| l | x-Ladungen |
x-berechnete Werte
Bei den x-berechneten Werten handelt es sich um lineare Kombinationen der x-Werte; sie enthalten die Streuung in den Prädiktoren, die vom PLS-Modell erklärt wird. Beobachtungen mit relativ kleinen x-berechneten Werten sind Ausreißer im x-Raum und werden vom Modell nicht gut erklärt.
Die Matrix der x-berechneten Werte, die der ursprünglichen x-Matrix ähnelt, ist eine (n × p)-Matrix, wobei n die Anzahl der Beobachtungen und p die Anzahl der Prädiktoren darstellt. Die x-berechneten Werte befinden sich auf derselben Skala wie die Prädiktoren.
Die Matrix der x-berechneten Werte wird anfänglich auf die Nullmatrix festgelegt. Nach der Berechnung der m-ten Komponente sowie der Vektoren der x-Werte und der x-Ladungen berechnet Minitab die x-berechneten Werte. Wenn die Anzahl der Komponenten gleich der Anzahl der Prädiktoren ist, ist der x-berechnete Wert gleich dem ursprünglichen Wert.
Formel

Anschließend berechnet Minitab die nicht standardisierten x-berechneten Werte, indem die standardisierten x-berechneten Werte mit der Standardabweichung der Prädiktorwerte multipliziert werden und der Mittelwert addiert wird.
Notation
| Begriff | Beschreibung |
|---|---|
| n | Anzahl der Beobachtungen |
| p | Anzahl der Prädiktoren |
| i | Anzahl der Beobachtungen von 1 bis n |
| j | Anzahl der Prädiktoren von 1 bis p |
| t | x-Werte |
| l | x-Ladungen |
y-Werte
Die y-Werte sind lineare Kombinationen der Antwortvariablen. Die y-Werte bilden eine n × m-Matrix. Die y-Werte stellen Projektionen der Beobachtungen auf die PLS-Komponenten dar.
Formel
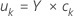
Notation
| Begriff | Beschreibung |
|---|---|
| n | Anzahl der Beobachtungen |
| m | Anzahl der Komponenten |
| k | Anzahl der Werte der Antwortvariablen von 1 bis r |
| Y | y-Matrix |
| c | y-Ladungen |
y-Ladungen
Die y-Ladungen sind die linearen Koeffizienten, die die Antwortvariablen mit den y-Werten verknüpfen. Die Werte der Ladungen geben die Relevanz der entsprechenden Antwortvariablen für die m-te Komponente an. Die y-Ladungen bilden eine r × m-Matrix.
Formel

Notation
| Begriff | Beschreibung |
|---|---|
| r | Anzahl der Werte der Antwortvariablen |
| m | Anzahl der Komponenten |
| i | Beobachtungen von 1 bis n |
| k | Werte der Antwortvariablen von 1 bis r |
| Y | Werte der Antwortvariablen |
| t | x-Werte |
y-Residuen
Die y-Residuen enthalten die verbleibende Streuung in den Antwortvariablen, die vom PLS-Modell nicht erklärt wird. Beobachtungen mit relativ großen y-Residuen sind Ausreißer im y-Raum und werden nicht gut erklärt.
Die y-Residuen sind die Differenzen zwischen den tatsächlichen Werten der Antwortvariablen und den y-berechneten Werten, und sie befinden sich auf derselben Skala wie die ursprünglichen Werte der Antwortvariablen. Die Matrix der y-Residuen ist, ähnlich wie die ursprüngliche y-Matrix, eine (n × r)-Matrix.
Die Matrix der y-Residuen wird anfänglich auf die Matrix der standardisierten y-Werte festgelegt. Nachdem Minitab die m-te Komponente sowie die Vektoren der x-Werte und der y-Ladungen berechnet hat, ermittelt Minitab die standardisierten y-Residuen.
Formel

Anschließend berechnet Minitab die nicht standardisierten y-Residuen, indem die standardisierten y-Residuen mit der Standardabweichung der entsprechenden Werte der Antwortvariablen multipliziert werden.
Notation
| Begriff | Beschreibung |
|---|---|
| n | Anzahl der Beobachtungen |
| r | Anzahl der Werte der Antwortvariablen |
| i | Beobachtungen von 1 bis n |
| k | Werte der Antwortvariablen von 1 bis r |
| t | x-Werte |
| c | y-Ladungen |
y-berechnete Werte
Bei den y-berechneten Werten handelt es sich um lineare Kombinationen der x-Werte; sie enthalten die Streuung in den Antwortvariablen, die vom PLS-Modell erklärt wird. Beobachtungen mit relativ kleinen y-berechneten Werten sind Ausreißer im y-Raum und werden nicht gut erklärt.
Die Matrix der y-berechneten Werte ist, ähnlich wie die ursprüngliche y-Matrix, eine (n x r)-Matrix. Die Matrix der y-berechneten Werte wird anfänglich auf eine Nullmatrix festgelegt. Nachdem Minitab die m-te Komponente sowie die Vektoren der x-Werte und der y-Ladungen berechnet hat, ermittelt Minitab die standardisierten y-berechneten Werte.
Formel

Anschließend berechnet Minitab die nicht standardisierten y-berechneten Werte, indem die standardisierten y-berechneten Werte mit der Standardabweichung der entsprechenden Werte der Antwortvariablen multipliziert werden und der Mittelwert addiert wird.
Notation
| Begriff | Beschreibung |
|---|---|
| n | Anzahl der Beobachtungen |
| r | Anzahl der Werte der Antwortvariablen |
| i | Beobachtungen von 1 bis n |
| k | Werte der Antwortvariablen von 1 bis r |
| t | x-Werte |
| c | y-Ladungen |
