In diesem Thema
Schritt 1. Bestimmen der Anzahl der Komponenten im Modell
Das Ziel bei der PLS besteht darin, ein Modell auszuwählen, das eine geeignete Anzahl von Komponenten enthält und gute Prognosefähigkeiten aufweist. Bei der Anpassung eines PLS-Modells können Sie eine Kreuzvalidierung durchführen, um die optimale Anzahl von Komponenten im Modell zu ermitteln. Bei der Kreuzvalidierung wählt Minitab das Modell mit dem höchsten prognostizierten R2 aus. Wenn Sie keine Kreuzvalidierung verwenden, können Sie die Anzahl der Komponenten angeben, die in das Modell eingebunden werden sollen, oder die Standardanzahl von Komponenten verwenden. Die Standardanzahl von Komponenten ist 10 oder, falls kleiner, die Anzahl der Prädiktoren in den Daten. Ermitteln Sie anhand der Regressionstabelle, wie viele Komponenten Minitab in das Modell eingebunden hat. Sie können auch das Modellauswahldiagramm überprüfen.
Wenn Sie die PLS verwenden, wählen Sie ein Modell mit der kleinsten Anzahl von Komponenten aus, die die Streuung in den Prädiktoren und Antwortvariablen hinreichend erklären. Um die für Ihre Daten am besten geeignete Anzahl von Komponenten zu ermitteln, untersuchen Sie die Modellauswahltabelle mit der x-Varianz, dem R2 und dem prognostizierten R2. Das prognostizierte R2 gibt die Prognosefähigkeiten des Modells an und wird nur angezeigt, wenn eine Kreuzvalidierung durchgeführt wird.
In einigen Fällen entscheiden Sie sich u. U. für ein anderes als das anfänglich von Minitab ausgewählte Modell. Wenn Sie die Kreuzvalidierung verwendet haben, vergleichen Sie das R2 und das prognostizierte R2. Betrachten Sie folgendes Beispiel: Wenn zwei Komponenten aus dem von Minitab ausgewählten Modell entfernt werden, verringert sich das prognostizierte R2 nur geringfügig. Da sich das prognostizierte R2 nur leicht verringert hat, ist das Modell nicht übermäßig angepasst, und möglicherweise entspricht es Ihren Daten besser.
Ein prognostiziertes R2, das wesentlich kleiner als R2 ist, kann auf eine übermäßige Anpassung des Modells hinweisen. Ein übermäßig angepasstes Modell liegt vor, wenn Sie Terme oder Komponenten für Effekte hinzufügen, die in der Grundgesamtheit unbedeutend sind, obwohl sie in den Stichprobendaten als wichtig erscheinen. Das Modell wird somit an die Stichprobendaten angepasst und ist daher möglicherweise beim Aufstellen von Prognosen für die Grundgesamtheit nicht nützlich.
Wenn Sie keine Kreuzvalidierung verwenden, können Sie die Werte der x-Varianz in der Modellauswahltabelle untersuchen, um zu ermitteln, wie viel der Streuung in der Antwortvariablen durch die einzelnen Modelle erklärt wird.
Methode
| Kreuzvalidierung | Eine auslassen |
|---|---|
| Auszuwertende Komponenten | Fest |
| Anzahl der ausgewerteten Komponenten | 10 |
| Anzahl der ausgewählten Komponenten | 4 |
Methode
| Kreuzvalidierung | Keine |
|---|---|
| Zu berechnende Komponenten | Fest |
| Anzahl der berechneten Komponenten | 10 |
Wichtigstes Ergebnis: Anzahl der Komponenten
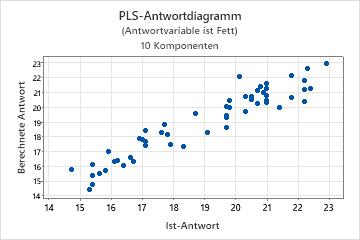
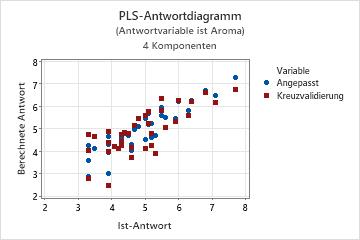
In diesen Ergebnissen ist in der ersten Regressionstabelle ersichtlich, dass die Kreuzvalidierung verwendet und das Modell mit vier Komponenten ausgewählt wurde. In der zweiten Regressionstabelle wird gezeigt, dass die Kreuzvalidierung nicht verwendet wurde. Minitab verwendet das Modell mit 10 Komponenten, also mit der Standardanzahl.
Modellauswahl und Validierung für Aroma
| Komponenten | X-Varianz | Fehler | R-Qd | PRESS | R-Qd(prog) |
|---|---|---|---|---|---|
| 1 | 0,158849 | 14,9389 | 0,637435 | 23,3439 | 0,433444 |
| 2 | 0,442267 | 12,2966 | 0,701564 | 21,0936 | 0,488060 |
| 3 | 0,522977 | 7,9761 | 0,806420 | 19,6136 | 0,523978 |
| 4 | 0,594546 | 6,6519 | 0,838559 | 18,1683 | 0,559056 |
| 5 | 5,8530 | 0,857948 | 19,2675 | 0,532379 | |
| 6 | 5,0123 | 0,878352 | 22,3739 | 0,456988 | |
| 7 | 4,3109 | 0,895374 | 24,0041 | 0,417421 | |
| 8 | 4,0866 | 0,900818 | 24,7736 | 0,398747 | |
| 9 | 3,5886 | 0,912904 | 24,9090 | 0,395460 | |
| 10 | 3,2750 | 0,920516 | 24,8293 | 0,397395 |
Wichtigste Ergebnisse: x-Varianz, R-Qd, R-Qd (prog)
In diesen Ergebnissen hat Minitab das Modell mit 4 Komponenten ausgewählt, bei dem der Wert des prognostizierten R2 ungefähr 56 % beträgt. Basierend auf der x-Varianz erklärt das Modell mit 4 Komponenten fast 60 % der Streuung der Prädiktoren. Bei steigender Anzahl von Komponenten erhört sich das R2, das prognostizierte R2 nimmt hingegen ab; dies deutet darauf hin, dass Modelle mit mehr Komponenten wahrscheinlich übermäßig angepasst sind.
Schritt 2: Bestimmen, ob die Daten Ausreißer oder Hebelwirkungspunkte enthalten
Um zu ermitteln, ob das Modell gut an die Daten angepasst ist, untersuchen Sie Diagramme auf Ausreißer, Hebelwirkungspunkte und andere Muster. Wenn Ihre Daten viele Ausreißer oder Hebelwirkungspunkte enthalten, liefert das Modell möglicherweise keine gültigen Prognosen.
- Ausreißer: Beobachtungen mit großen standardisierten Residuen liegen außerhalb der horizontalen Referenzlinien im Diagramm.
- Hebelwirkungspunkte: Beobachtungen mit Hebelwirkungswerten weisen x-Werte weit entfernt von null auf und liegen rechts neben der vertikalen Referenzlinie.
Weitere Informationen zum Diagramm der Residuen im Vergleich mit der Hebelwirkung finden Sie unter Grafiken für Regression der partiellen kleinsten Quadrate.
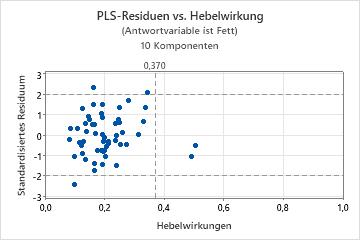
- Ein nichtlineares Muster in den Punkten verweist darauf, dass das Modell möglicherweise nicht gut an die Daten angepasst ist oder die Daten u. U. nicht präzise prognostiziert.
- Wenn Sie eine Kreuzvalidierung ausführen, verweisen große Differenzen zwischen angepassten und kreuzvalidierten Werten auf einen Hebelwirkungspunkt.
Schritt 3. Validieren des PLS-Modells mit einem Testdatensatz
Die PLS-Regression wird oft in zwei Schritten durchgeführt. Im ersten Schritt, auch als Training bezeichnet, wird ein PLS-Regressionsmodell für einen Beispieldatensatz (auch als Trainingsdatensatz bezeichnet) berechnet. Im zweiten Schritt wird dieses Modell mit einem anderen Datensatz validiert, der auch als Testdatensatz bezeichnet wird. Um das Modell mit dem Testdatensatz zu validieren, geben Sie die Spalten der Testdaten im Unterdialogfeld Prognose ein. Minitab berechnet für jede Beobachtung im Testdatensatz neue Werte der Antwortvariablen und vergleicht den prognostizierten mit dem tatsächlichen Wert der Antwortvariablen. Auf der Grundlage des Vergleichs berechnet Minitab das Test-R2, das die Fähigkeit des Modells zum Prognostizieren von neuen Werten der Antwortvariablen angibt. Höhere Werte des Test-R2 geben eine bessere Prognosefähigkeit des Modells an.
Wenn Sie die Kreuzvalidierung verwenden, vergleichen Sie das Test-R2 mit dem prognostizierten R2. Im Idealfall sollten diese Werte einander ähneln. Ein Test-R2, das signifikant kleiner als das prognostizierte R2 ist, weist darauf hin, dass die Kreuzvalidierung hinsichtlich der Prognosefähigkeit des Modells zu optimistisch ist oder die beiden Datenstichproben aus verschiedenen Grundgesamtheiten stammen.
Wenn der Testdatensatz keine Werte der Antwortvariablen enthält, berechnet Minitab kein Test-R2.
Prognostizierte Antwort für neue Beobachtungen unter Verwendung des Modells für Fett
| Zeile | Anpassung | SE Anpassung | 95%-KI | 95%-PI |
|---|---|---|---|---|
| 1 | 18,7372 | 0,378459 | (17,9740; 19,5004) | (16,8612; 20,6132) |
| 2 | 15,3782 | 0,362762 | (14,6466; 16,1098) | (13,5149; 17,2415) |
| 3 | 20,7838 | 0,491134 | (19,7933; 21,7743) | (18,8044; 22,7632) |
| 4 | 14,3684 | 0,544761 | (13,2698; 15,4670) | (12,3328; 16,4040) |
| 5 | 16,6016 | 0,348485 | (15,8988; 17,3044) | (14,7494; 18,4538) |
| 6 | 20,7471 | 0,472648 | (19,7939; 21,7003) | (18,7861; 22,7080) |
Wichtigstes Ergebnis: Test-R2
In diesen Ergebnissen beträgt das Test-R2 ungefähr 76 %. Das prognostizierte R2 für den ursprünglichen Datensatz beträgt ungefähr 78 %. Da diese Werte ähnlich sind, können Sie schlussfolgern, dass das Modell eine angemessene Prognosefähigkeit aufweist.
