In diesem Thema
Modellauswahldiagramm
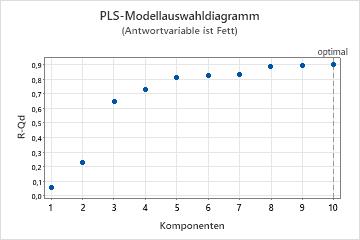
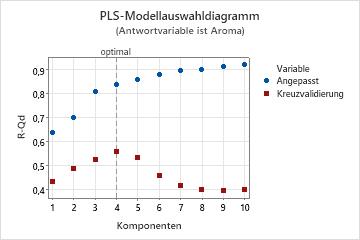
Das Modellauswahldiagramm ist ein Streudiagramm der Werte von R2 und dem prognostizierten R2 als Funktion der Anzahl der Komponenten, die angepasst oder kreuzvalidiert wurden. Dabei handelt es sich um eine grafische Darstellung der Modellauswahl- und Validierungstabelle. Wenn keine Kreuzvalidierung verwendet wird, werden die Werte des prognostizierten R2 im Diagramm nicht angezeigt. Minitab stellt pro Antwortvariable ein Modellauswahldiagramm bereit.
Interpretation
Anhand dieses Diagramms können Sie die Modellierungs- und Prognosefähigkeiten der verschiedenen Modelle vergleichen, um die geeignete Anzahl von Komponenten zu ermitteln, die im Modell beibehalten werden sollen. Die vertikale Linie im Diagramm gibt die Anzahl der Komponenten an, die Minitab für das PLS-Modell ausgewählt hat.
Antwortdiagramm
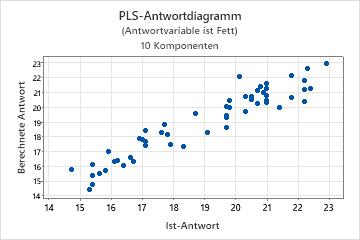
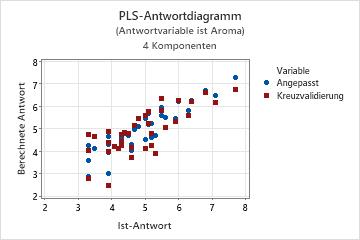
Das Antwortdiagramm ist ein Streudiagramm der angepassten Werte im Vergleich zu den tatsächlichen Werten der Antwortvariablen. Wenn Sie eine Kreuzvalidierung ausführen, enthält das Diagramm außerdem die angepassten Werte im Vergleich zu den kreuzvalidierten angepassten Werten. Minitab stellt ein Antwortdiagramm pro Antwortvariable bereit.
Interpretation
- Ein nichtlineares Muster in den Punkten verweist darauf, dass das Modell möglicherweise nicht gut an die Daten angepasst ist oder die Daten u. U. nicht präzise prognostiziert.
- Wenn Sie eine Kreuzvalidierung ausführen, verweisen große Differenzen zwischen angepassten und kreuzvalidierten Werten auf einen Hebelwirkungspunkt.
Ein Modell mit hervorragenden Prognosefähigkeiten weist in der Regel eine Steigung von 1 auf und schneidet die y-Achse bei 0.
Koeffizientendiagramm
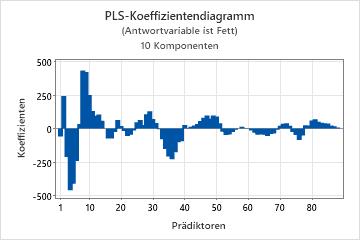
Das Koeffizientendiagramm ist ein projiziertes Streudiagramm, in dem die nicht standardisierten Koeffizienten für die einzelnen Prädiktoren dargestellt werden. Minitab stellt ein Koeffizientendiagramm pro Antwortvariable bereit.
Interpretation
Verwenden Sie das Koeffizientendiagramm und die ausgegebenen Regressionskoeffizienten, um Vorzeichen und Größe der Koeffizienten für die einzelnen Prädiktoren zu vergleichen. Dieses Diagramm erleichtert es Ihnen, rasch zu ermitteln, welche Prädiktoren im Modell mehr oder weniger wichtig sind.
Da im Diagramm nicht standardisierte Koeffizienten angezeigt werden, können Sie Vergleiche bezüglich der Größe der Beziehungen zwischen Prädiktoren und der Antwortvariablen nur anstellen, wenn sich die Prädiktoren auf derselben Skala befinden (z. B. bei Spektraldaten). Andernfalls empfiehlt es sich, das standardisierte Koeffizientendiagramm oder das Ladungsdiagramm zu verwenden, um die Gewichtungen der Prädiktoren zum Berechnen der Komponenten zu vergleichen.
Std.-Koeffizientendiagramm
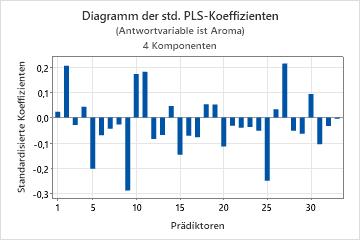
Das Koeffizientendiagramm ist ein projiziertes Streudiagramm, in dem die standardisierten Koeffizienten für die einzelnen Prädiktoren dargestellt werden. Minitab stellt ein standardisiertes Koeffizientendiagramm pro Antwortvariable bereit.
Interpretation
Vergleichen Sie anhand dieses Diagramms und den ausgegebenen Regressionskoeffizienten Vorzeichen und Größe der Koeffizienten für die einzelnen Prädiktoren. Dieses Diagramm erleichtert Ihnen das schnelle Ermitteln von Prädiktoren, die im Modell mehr oder weniger wichtig sind.
Da im Diagramm standardisierte Koeffizienten angezeigt werden, können Sie Vergleiche bezüglich der Größe der Beziehungen zwischen Prädiktoren und der Antwortvariablen anstellen, selbst wenn sich die Prädiktoren nicht auf derselben Skala befinden.
Wenn sich die Prädiktoren auf derselben Skala befinden, ähneln die Muster der Koeffizienten in standardisierten und nicht standardisierten Diagrammen einander. Diese Diagramme sehen jedoch u. U. nicht identisch aus, da die Prädiktoren stark korrelieren, wodurch die Koeffizienten instabil werden. Ein weiterer Grund dafür sind die Differenzen zwischen den Standardabweichungen der Stichproben und den Standardabweichungen der Grundgesamtheit.
Distanzdiagramm
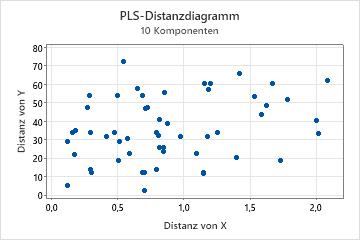
Das Distanzdiagramm ist ein Streudiagramm der Distanz der einzelnen Beobachtungen vom x- und y-Modell. Mit den Distanzen vom y-Modell wird gemessen, wie gut die Anpassung an die Beobachtung im y-Raum ist. Mit den Distanzen vom x-Modell wird gemessen, wie gut die Anpassung an die Beobachtung im x-Raum ist.
Interpretation
Untersuchen Sie dieses Diagramm auf Punkte, die eine größere Distanz als andere Punkte auf der x- bzw. y-Achse aufweisen. Beobachtungen mit größeren Distanzen vom y-Modell können Ausreißer sein, und Beobachtungen mit größeren Distanzen vom x-Modell können Hebelwirkungspunkte sein.
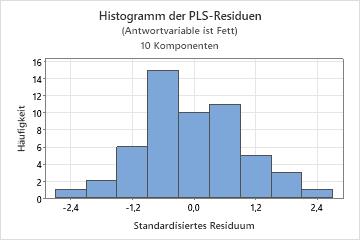
Histogramm der Residuen
Im Histogramm der standardisierten Residuen wird die Verteilung der standardisierten Residuen für alle Beobachtungen veranschaulicht.
Interpretation
| Muster | Mögliche Bedeutung des Musters |
|---|---|
| Ein langer Randbereich in einer Richtung | Schiefe |
| Ein Balken weit entfernt von den anderen Balken | Ein Ausreißer |
Da die Darstellung eines Histogramms von der Anzahl der Intervalle abhängt, die zum Gruppieren der Daten verwendet werden, ist ein Histogramm nicht geeignet, um zu beurteilen, ob die Residuen normalverteilt sind. Verwenden Sie stattdessen ein Wahrscheinlichkeitsnetz für Normalverteilung. Ein Histogramm ist am effektivsten, wenn Sie über mindestens ca. 20 Datenpunkte verfügen. Wenn die Stichprobe zu klein ist, enthalten die einzelnen Balken im Histogramm keine ausreichende Menge an Datenpunkten, um Schiefe und Ausreißer zuverlässig darzustellen.
Wahrscheinlichkeitsnetz (Normal) für Residuen
Das Wahrscheinlichkeitsnetz (Normal) für Residuen stellt die standardisierten Residuen im Vergleich zu den Werten dar, die bei Vorliegen einer Normalverteilung erwartet würden.
Interpretation
Verwenden Sie das Wahrscheinlichkeitsnetz (Normal) der Residuen, um die Annahme zu überprüfen, dass die Residuen normalverteilt sind. Die Residuen im Wahrscheinlichkeitsnetz für Normalverteilung sollten ungefähr einer Geraden folgen.
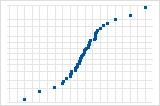
Die S-Kurve deutet auf eine Verteilung mit langen Randbereichen hin.
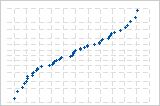
Die invertierte S-Kurve deutet auf eine Verteilung mit kurzen Randbereichen hin.
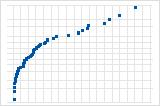
Eine Abwärtskurve deutet auf eine rechtsschiefe Verteilung hin.
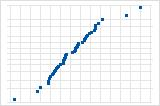
Wenige Punkte, die abseits der Linie liegen, deuten auf eine Verteilung mit Ausreißern hin.
Wenn Sie ein nicht normalverteiltes Muster feststellen, prüfen Sie das Modell anhand der übrigen Residuendiagramme auf andere Probleme, z. B. auf fehlende Terme oder einen Effekt der chronologischen Reihenfolge. Wenn die Residuen keiner Normalverteilung folgen, sind die Konfidenzintervalle und p-Werte möglicherweise ungenau.
Residuen vs. Anpassungen
Im Diagramm der Residuen im Vergleich mit den Anpassungen werden die standardisierten Residuen auf der y-Achse und die angepassten Werte auf der x-Achse abgetragen.
Interpretation
Verwenden Sie das Diagramm der Residuen im Vergleich zu den Anpassungen, um die Annahme zu überprüfen, dass die Residuen zufällig verteilt sind und eine konstante Varianz aufweisen. Im Idealfall sollten die Punkte zufällig auf beiden Seiten von null verteilt sein, und es sollten keine Muster in den Punkten erkennbar sein.
| Muster | Mögliche Bedeutung des Musters |
|---|---|
| Aufgefächerte oder ungleichmäßig gestreute Residuen für die angepassten Werte | Nicht konstante Varianz |
| Krümmung | Ein fehlender Term höherer Ordnung |
| Ein weit von null entfernt liegender Punkt | Ein Ausreißer |
| Ein in x-Richtung weit von den anderen Punkten entfernter Punkt | Ein einflussreicher Punkt |

Diagramm mit Ausreißer
Einer der Punkte ist viel größer als alle anderen Punkte. Daher handelt es sich bei dem Punkt um einen Ausreißer. Wenn zu viele Ausreißer auftreten, ist das Modell möglicherweise nicht akzeptabel. Versuchen Sie nach Möglichkeit, die Ursache von Ausreißern zu ermitteln. Korrigieren Sie sämtliche Dateneingabe- oder Messfehler. Erwägen Sie, Datenwerte zu entfernen, die auf ungewöhnliche, einmalige Ereignisse (Ausnahmebedingungen) zurückzuführen sind. Wiederholen Sie anschließend die Analyse.
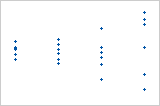
Diagramm mit nicht konstanter Varianz
Die Varianz der Residuen nimmt mit den angepassten Werten zu. Beachten Sie, dass sich bei zunehmenden Werten der Anpassungen die Streuung der Residuen verbreitert. Dieses Muster weist darauf hin, dass die Varianzen der Residuen ungleich (nicht konstant) sind.
Residuen vs. Hebelwirkung
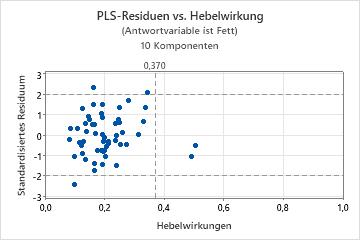
Das Diagramm der Residuen im Vergleich zu den Hebelwirkungen ist ein Streudiagramm der standardisierten Residuen im Vergleich zu den Hebelwirkungen der einzelnen Beobachtungen.
Interpretation
- Ausreißer: Beobachtungen mit standardisierten Residuen größer als +/–2, die außerhalb der horizontalen Referenzlinien im Diagramm liegen.
- Hebelwirkungspunkte: Beobachtungen mit Hebelwirkungswerten größer als 2m/n, wobei m der Anzahl der Komponenten und n der Anzahl der Beobachtungen entspricht, die als extrem angesehen werden. Sie weisen weit von null entfernte x-Werte auf und befinden sich rechts neben der vertikalen Referenzlinie, die bei 2m/n auf der x-Achse liegt. Wenn 2m/n größer als 1 ist, wird die Referenzlinie im Diagramm nicht angezeigt, weil Hebelwirkungswerte immer zwischen 0 und 1 liegen.
Residuen vs. Reihenfolge
Das Diagramm der Residuen im Vergleich mit der Reihenfolge zeigt die standardisierten Residuen in der Reihenfolge an, in der die Daten erfasst wurden.
Interpretation
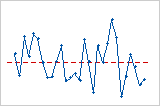
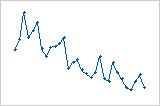
Trend
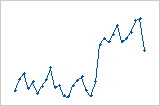
Shift
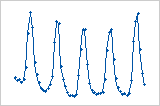
Zyklus
Scoreplot
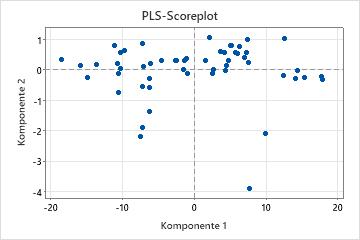
Das Scoreplot ist ein Streudiagramm der x-Werte aus der ersten und der zweiten Komponente im Modell.
Interpretation
Wenn die ersten beiden Komponenten den größten Teil der Streuung in den Prädiktoren erklären, spiegelt die Konfiguration der Punkte in diesem Diagramm die ursprüngliche mehrdimensionale Konfiguration der Daten weitgehend wider. Um zu überprüfen, welcher Streuungsgrad in den Prädiktoren durch das Modell erklärt wird, untersuchen Sie die Werte der x-Varianz in der Modellauswahl- und Validierungstabelle. Wenn der Wert für die x-Varianz hoch ist, erklärt das Modell einen signifikanten Teil der Streuung der Prädiktoren.
- Hebelwirkungspunkte: Punkte, die weit entfernt von der Mehrheit der Punkte im Diagramm liegen, können Hebelwirkungspunkte sein und sich signifikant auf die Ergebnisse auswirken.
- Cluster: Gruppen von Punkten können auf zwei oder mehr verschiedene Verteilungen in den Daten verweisen, die mit anderen Modellen möglicherweise besser beschrieben werden können.
Hinweis
Wenn das Modell mehr als zwei Komponenten enthält, empfiehlt es sich möglicherweise, die x-Werte der anderen Komponenten mit Hilfe von Streudiagramm darzustellen. Speichern Sie dafür die Matrix der x-Werte, und kopieren Sie sie anschließend in Spalten, indem Sie auswählen. Wenn das Modell nur eine Komponente enthält, wird dieses Diagramm in der Ausgabe nicht angezeigt.
3D-Scoreplot
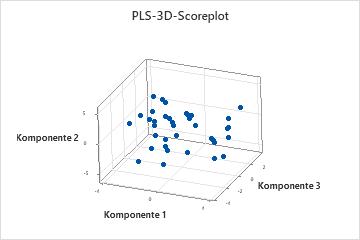
Das 3D-Scoreplot ist ein dreidimensionales Streudiagramm der x-Werte aus der ersten, zweiten und dritten Komponente im Modell. Wenn die ersten drei Komponenten den größten Teil der Streuung in den Prädiktoren erklären, spiegelt die Konfiguration der Punkte in diesem Diagramm die ursprüngliche mehrdimensionale Konfiguration der Daten weitgehend wider. Um zu überprüfen, welcher Streuungsgrad durch das Modell erklärt wird, untersuchen Sie die Werte der x-Varianz in der Modellauswahl- und Validierungstabelle. Wenn der Wert für die x-Varianz hoch ist, erklärt das Modell einen signifikanten Teil der Streuung der Prädiktoren.
Interpretation
- Hebelwirkungspunkte: Punkte, die weit entfernt von der Mehrheit der Punkte im Diagramm liegen, können Hebelwirkungspunkte sein und sich signifikant auf die Ergebnisse auswirken.
- Cluster: Gruppen von Punkten können auf zwei oder mehr verschiedene Verteilungen in den Daten verweisen, die mit anderen Modellen möglicherweise besser beschrieben werden können.
Darüber hinaus sollten Sie die 3D-Grafikwerkzeuge verwenden, mit denen Sie ein Diagramm drehen können, so dass Sie es aus verschiedenen Perspektiven betrachten können. Dadurch erhalten Sie ein umfassenderes Bild der Daten, und Sie können Hebelwirkungspunkte und Cluster von Punkten präziser erkennen.
Ladungsdiagramm
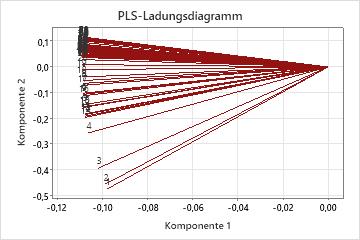
Das Ladungsdiagramm ist ein Streudiagramm der Prädiktoren, die auf die erste und die zweite Komponente im Modell projiziert wurden. Es veranschaulicht die x-Ladungen für die zweite Komponente im Vergleich zu den x-Ladungen der ersten Komponente. Jeder Punkt, der jeweils einen Prädiktor darstellt, ist im Diagramm mit (0,0) verbunden.
Interpretation
Im Ladungsdiagramm wird dargestellt, wie wichtig die Prädiktoren für die ersten beiden Komponenten sind; es ist besonders hilfreich, wenn sich die Prädiktoren auf verschiedenen Skalen befinden. Wenn die Komponenten den größten Teil der x-Varianz erklären, was in der Modellauswahl- und Validierungstabelle veranschaulicht wird, gibt das Ladungsdiagramm an, wie wichtig die Prädiktoren im x-Raum sind. Beim Untersuchen der Bedeutung der Prädiktoren für das gesamte Modell müssen Sie außerdem berücksichtigen, welchen Teil der Varianz in der Antwortvariablen die Komponenten erklären. Untersuchen Sie hierzu die Werte von R2 und dem prognostiziertem R2 in der Modellauswahl- und Validierungstabelle.
- Winkel zwischen den Linien, die die Korrelation zwischen den Prädiktoren darstellen. Kleinere Winkel verweisen darauf, dass die Prädiktoren stark korrelieren.
- Prädiktoren mit längeren Linien, die in der ersten oder zweiten Komponente größere Ladungen aufweisen und im Modell wichtiger sind.
Hinweis
Wenn das Modell mehr als zwei Komponenten enthält, empfiehlt es sich möglicherweise, die x-Ladungen der anderen Komponenten mit Hilfe von Streudiagramm darzustellen. Speichern Sie dafür die Matrix der x-Ladungen, und kopieren Sie sie anschließend in Spalten, indem Sie auswählen.
Residuen-x-Diagramm
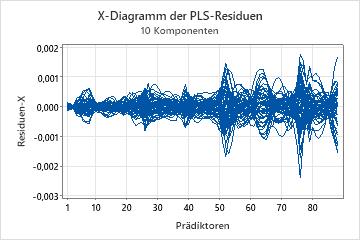
Das Residuen-x-Diagramm ist ein Liniendiagramm der x-Residuen im Vergleich zu den Prädiktoren. Jede Linie stellt eine Beobachtung dar und verfügt über ebenso viele Punkte wie Prädiktoren.
Interpretation
Ermitteln Sie anhand des Residuenmatrix-x-Diagramms Beobachtungen oder Prädiktoren, die vom Modell mangelhaft beschrieben werden. Dieses Diagramm ist am nützlichsten, wenn sich die Prädiktoren auf derselben Skala befinden.
- Wenn sich die Linien am selben Punkt auf der x-Achse voneinander trennen, beschreibt das Modell den Prädiktor an diesem Punkt schlecht.
- Wenn eine Linie im Diagramm von den anderen Linien abweicht, beschreibt das Modell die von dieser Linie dargestellte Beobachtung schlecht.
Untersuchen Sie anhand des Residuenmatrix-x-Diagramms allgemeine Muster in den Residuen, und ermitteln Sie Problembereiche. Untersuchen Sie anschließend die x-Residuen in der Ausgabe, um zu ermitteln, welche Beobachtungen und Prädiktoren vom Modell nicht angemessen beschrieben werden.
Berechnetes X-Diagramm
Das berechnete x-Diagramm ist ein Liniendiagramm der x-berechneten Werte im Vergleich zu den Prädiktoren. Jede Linie stellt eine Beobachtung dar und verfügt über ebenso viele Punkte wie Prädiktoren.
Interpretation
Verwenden Sie dieses Diagramm, um Beobachtungen oder Prädiktoren zu ermitteln, die vom Modell mangelhaft beschrieben werden. Dieses Diagramm ist am nützlichsten, wenn sich die Prädiktoren auf derselben Skala befinden.
Das berechnete x-Diagramm ergänzt das Residuen-x-Diagramm. Die Summe beider Diagramme ergibt ein Diagramm der ursprünglichen Werte der Prädiktorvariablen. Ein Prädiktor mit x-berechneten Werten, die erheblich kleiner oder größer als die ursprünglichen x-Werte sind, wird vom Modell nicht gut beschrieben.