Methoden und Formeln für Orthogonale Regression

Das Modell für den Messfehler lautet:

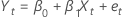
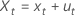
Bei der orthogonalen Regression ist die Linie am besten angepasst, bei der die gewichteten orthogonalen Distanzen von den Diagrammpunkten zur Linie minimiert sind. Wenn das Fehlervarianzverhältnis 1 beträgt, sind die gewichteten Distanzen euklidische Distanzen.

Notation

Begriff	Beschreibung
Yt	beobachteter Wert der Antwortvariablen
β0	Schnittpunkt mit y-Achse
β1	Steigung
Xt	beobachteter Prädiktor
xt	tatsächlicher und nicht beobachteter Wert des Prädiktors
et, ut	Messfehler; et, ut sind unabhängig mit dem Mittelwert 0 und den Fehlervarianzen δe2 und δu2

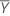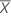Sei der Stichprobenmittelwert (, ), und sei die Kovarianzmatrix der Stichprobe:

m_ZZ ist eine symmetrische (2 x 2)-Matrix:

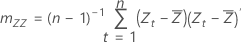
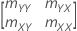
Notation

Begriff	Beschreibung
Zt	(Yt, Xt)
n	Stichprobenumfang

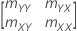
Wenn das Element m_XY der Kovarianzmatrix der Stichprobe ungleich 0 ist, dann gilt:

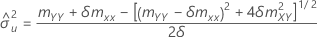
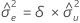
Wenn m_XY = 0 und m_YY < δm_XX, dann gilt:

Wenn m_XY = 0 und m_YY > δm_XX, sind die verbleibenden Parameterschätzwerte nicht definiert.

Notation

Begriff	Beschreibung
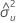	geschätzte Fehlervarianz für X
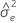	geschätzte Fehlervarianz für Y
δ	Verhältnis der Fehlervarianzen
mXY	Element der Kovarianzmatrix der Stichprobe
mYY	Element der Kovarianzmatrix der Stichprobe
mXX	Element der Kovarianzmatrix der Stichprobe

Wenn das Element m_XY der Kovarianzmatrix der Stichprobe ungleich 0 ist, dann gilt:

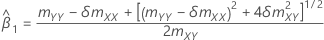
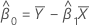
Wenn m_xy = 0 und m_yy < δm _xx, dann gilt:

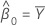
Wenn m_xy = 0 und m_yy > δm_xx, sind die verbleibenden Parameterschätzwerte nicht definiert.

Notation

Begriff	Beschreibung
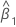	geschätzte Steigung
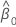	geschätzter Schnittpunkt mit der y-Achse
mxy	Element der Kovarianzmatrix der Stichprobe
myy	Element der Kovarianzmatrix der Stichprobe
δ	Verhältnis der Fehlervarianzen
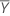	Mittelwert der Antwortvariablen
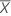	Mittelwert des Prädiktors

Eine Schätzung der Kovarianzmatrix der approximierten Verteilung des Schnittpunkts mit der y-Achse und der Steigung:

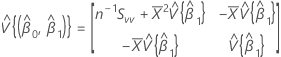
Dabei gilt Folgendes:

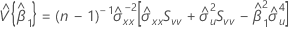
und

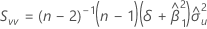
Wenn m_XY ungleich 0 ist:

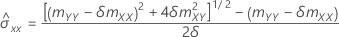
Wenn m_XY gleich 0 und m_YY < δm_XX ist:

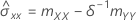
Notation

Begriff	Beschreibung
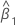	geschätzte Steigung
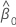	geschätzter Schnittpunkt mit der y-Achse
mXY	Element der Kovarianzmatrix der Stichprobe
mYY	Element der Kovarianzmatrix der Stichprobe
mXX	Element der Kovarianzmatrix der Stichprobe
δ	Verhältnis der Fehlervarianzen
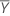	Mittelwert der Antwortvariablen
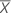	Mittelwert des Prädiktors

Das 100(1 – α)%-Konfidenzintervall für β₀ lautet:

Dabei gilt Folgendes:

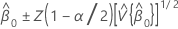
Z (1 – α / 2) ist das 100 * (1 – α / 2 )-te Perzentil der Standardnormalverteilung

und

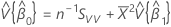, was ein Element der Kovarianzmatrix der approximierten Verteilung ist.

Notation

Begriff	Beschreibung
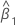	geschätzte Steigung
	geschätzter Schnittpunkt mit der y-Achse
α	Signifikanzniveau

Das 100(1 – α)%-Konfidenzintervall für β₁ lautet:

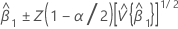
Dabei gilt Folgendes:

Z(1 – α / 2) ist das 100 * (1 – α / 2 )-te Perzentil der Standardnormalverteilung

und

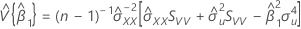
Notation

Begriff	Beschreibung
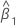	geschätzte Steigung
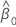	geschätzter Schnittpunkt mit der y-Achse
α	Signifikanzniveau

Der angepasste Wert für den Prädiktor x in der orthogonalen Regression lautet:

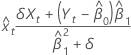
Notation

Begriff	Beschreibung
δ	Verhältnis der Fehlervarianzen
Yt	t-ter Wert der Antwortvariablen
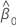	geschätzter Schnittpunkt mit der y-Achse
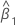	geschätzte Steigung

Der angepasste Wert für die Antwortvariable y in der orthogonalen Regression lautet:

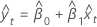
Notation

Begriff	Beschreibung
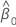	geschätzter Schnittpunkt mit der y-Achse
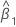	geschätzte Steigung
	t-ter angepasster Wert für x

In der orthogonalen Regression wird das Residuum einer Beobachtung wie folgt ausgedrückt:

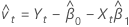
Notation

Begriff	Beschreibung
Yt	t-ter Wert der Antwortvariablen
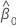	Schnittpunkt mit y-Achse
Xt	t-ter Prädiktorwert
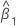	Steigung

Das standardisierte Residuum ist hilfreich beim Identifizieren von Ausreißern. Es wird folgendermaßen berechnet:

Dabei gilt Folgendes:

Notation

Begriff	Beschreibung
	Residuum
	Standardabweichung des Residuums
δ	Fehlervarianzverhältnis
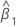	geschätzte Steigung
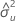	geschätzte Fehlervarianz für x

Der Prädiktor von Y_{n + 1} ist:

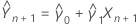
Dabei gilt Folgendes:

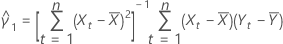
und

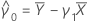
Notation

Begriff	Beschreibung
Xt	t-ter Prädiktorwert
	Mittelwert des Prädiktors
Yt	t-ter Wert der Antwortvariablen
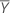	Mittelwert der Antwortvariablen

Dabei gilt Folgendes:

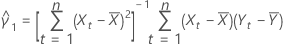
Notation

Begriff	Beschreibung
myy	Varianz der Stichprobe von Y
mxy	Stichprobenkovarianz zwischen den Zufallsvariablen X und Y