In diesem Thema
Diagramm mit Anpassungslinie
Das Diagramm mit der Anpassungslinie zeigt die Antwort- und Prädiktordaten. Das Diagramm enthält die Linie der orthogonalen Regression, die die Gleichung der orthogonalen Regression darstellt.
Zudem kann auch die Anpassungslinie, die nach der Methode der kleinsten Quadrate berechnet wird, zu Vergleichszwecken im Diagramm angezeigt werden. Größere Differenzen zwischen den Linien zeigen, wie stark die Ergebnisse davon abhängen, ob Sie Unsicherheiten in den Werten der Prädiktorvariable berücksichtigen. Die Werte der kleinsten Quadrate entsprechen den prognostizierten Werten für die orthogonale Regression, Sie können also auch die Linie der kleinsten Quadrate zur Untersuchung der prognostizierten Werte verwenden.
Interpretation
- Die Stichprobe enthält eine angemessene Anzahl von Beobachtungen über die gesamte Spannweite aller Prädiktorwerte.
- Die Stichprobe enthält keine Krümmung, an die das Modell nicht angepasst ist.
- Die Stichprobe enthält keine Ausreißer, die sich stark auf die Ergebnisse auswirken können. Versuchen Sie, die Ursache von Ausreißern zu ermitteln. Korrigieren Sie alle erkennbaren Dateneingabe- oder Messfehler. Erwägen Sie, Datenwerte zu entfernen, die auf ungewöhnliche, einmalige Ereignisse (Ausnahmebedingungen) zurückzuführen sind. Wiederholen Sie anschließend die Analyse.
Die orthogonale Regression findet häufig Anwendung in der klinischen Chemie und in Laboreinrichtungen, wenn festgestellt werden soll, ob zwei Instrumente oder zwei Methoden vergleichbare Messwerte liefern.
Dieses Diagramm zeigt ein Beispiel für Messwerte von zwei Instrumenten oder Methoden, die vergleichbar sind. Die Punkte folgen der angepassten Linie mit minimaler Streuung und ohne ein Muster, das systematische Differenzen zwischen den Methoden erkennen ließe.
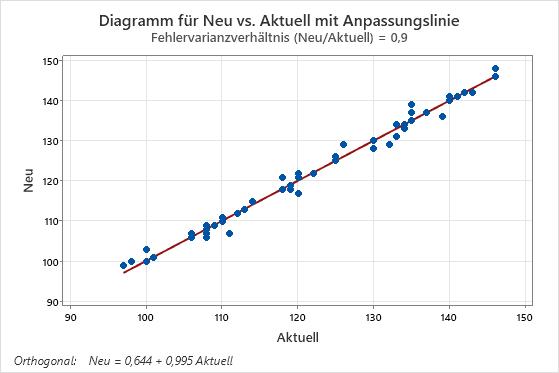
In den nachfolgenden Ergebnissen liefern die Konfidenzintervalle der Koeffizienten keine Hinweise darauf, dass sich die Messwerte der beiden Instrumente unterscheiden. Das Diagramm zeigt jedoch, dass einige Punkte nicht dicht an der Linie liegen, was darauf hinweist, dass die Messwerte der beiden Instrumente nicht vergleichbar sind. Da die Daten nicht zur Gleichung passen, wird in der Regel geschlussfolgert, dass sich die Instrumente unterscheiden.
Koeffizienten
| Prädiktor | Koef | SE Koef | z | p | Approx. 95%-KI |
|---|---|---|---|---|---|
| Konstante | -0,00000 | 0,215424 | -0,0000 | 1,000 | (-0,422224; 0,42222) |
| Neu | 1,00000 | 0,517586 | 1,9320 | 0,053 | (-0,014450; 2,01445) |
Histogramm der Residuen
Im Histogramm der Residuen wird die Verteilung der Residuen für alle Beobachtungen veranschaulicht.
Interpretation
| Muster | Mögliche Bedeutung des Musters |
|---|---|
| Ein langer Randbereich in einer Richtung | Schiefe |
| Ein Balken weit entfernt von den anderen Balken | Ein Ausreißer |
Die orthogonale Regression wird oft in der klinischen Chemie oder in Laboratorien verwendet, um zu untersuchen, ob zwei Instrumente oder Methoden gleich messen. Wenn das Modell die Annahmen nicht erfüllt, kann eine Erklärung hierfür sein, dass die Methoden nicht gleich messen.
Da die Darstellung eines Histogramms von der Anzahl der Intervalle abhängt, mit denen die Daten gruppiert werden, verwenden Sie ein Histogramm nicht, um die Normalverteilung der Residuen zu beurteilen. Verwenden Sie stattdessen ein Wahrscheinlichkeitsnetz für Normalverteilung.
Ein Histogramm ist am effektivsten, wenn Sie über mindestens ca. 20 Datenpunkte verfügen. Wenn die Stichprobe zu klein ist, enthalten die einzelnen Balken im Histogramm keine ausreichende Menge an Datenpunkten, um Schiefe und Ausreißer zuverlässig darzustellen.
Wahrscheinlichkeitsnetz (Normal) für Residuen
Das Wahrscheinlichkeitsnetz (Normal) für Residuen stellt die Residuen im Vergleich zu den Werten dar, die bei Vorliegen einer Normalverteilung erwartet würden.
Interpretation
Verwenden Sie das Wahrscheinlichkeitsnetz (Normal) der Residuen, um die Annahme zu überprüfen, dass die Residuen normalverteilt sind. Die Residuen im Wahrscheinlichkeitsnetz für Normalverteilung sollten ungefähr einer Geraden folgen.
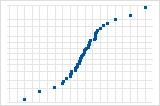
Die S-Kurve deutet auf eine Verteilung mit langen Randbereichen hin.
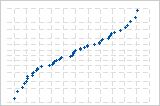
Die invertierte S-Kurve deutet auf eine Verteilung mit kurzen Randbereichen hin.
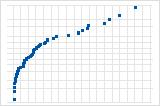
Eine Abwärtskurve deutet auf eine rechtsschiefe Verteilung hin.
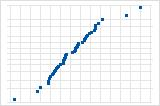
Wenige Punkte, die abseits der Linie liegen, deuten auf eine Verteilung mit Ausreißern hin.
Die orthogonale Regression wird oft in der klinischen Chemie oder in Laboratorien verwendet, um zu untersuchen, ob zwei Instrumente oder Methoden gleich messen. Wenn Sie ein nicht normalverteiltes Muster feststellen, kann eine Erklärung hierfür sein, dass die Methoden nicht gleich messen. Untersuchen Sie außerdem die anderen Residuendiagramme auf andere Probleme mit dem Modell, z. B. einen Effekt aufgrund der zeitlichen Reihenfolge. Wenn die Residuen keiner Normalverteilung folgen, sind die Konfidenzintervalle und p-Werte möglicherweise ungenau.
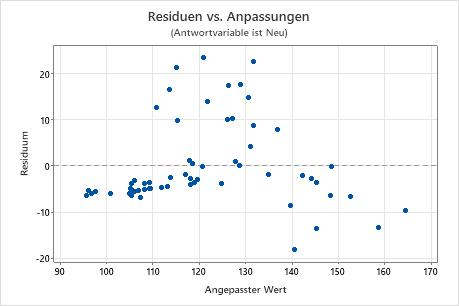
Residuen vs. Anpassungen
Im Diagramm der Residuen im Vergleich zu den Anpassungen werden die Residuen auf der y-Achse und die angepassten Werte für den Prädiktor auf der x-Achse abgetragen.
Die orthogonale Regression wird oft in der klinischen Chemie oder in Laboratorien verwendet, um zu untersuchen, ob zwei Instrumente oder Methoden gleich messen. Wenn das Modell die Annahmen nicht erfüllt, kann eine Erklärung hierfür sein, dass die Methoden nicht gleich messen.
Interpretation
Verwenden Sie das Diagramm der Residuen im Vergleich zu den Anpassungen, um die Annahme zu überprüfen, dass die Residuen zufällig verteilt sind und eine konstante Varianz aufweisen. Im Idealfall sollten die Punkte zufällig auf beiden Seiten von null verteilt sein, und es sollten keine Muster in den Punkten erkennbar sein.
| Muster | Mögliche Bedeutung des Musters |
|---|---|
| Aufgefächerte oder ungleichmäßig gestreute Residuen für die angepassten Werte | Nicht konstante Varianz |
| Krümmung | Ein fehlender Term höherer Ordnung |
| Ein weit von null entfernt liegender Punkt | Ein Ausreißer |
| Ein in x-Richtung weit von den anderen Punkten entfernter Punkt | Ein einflussreicher Punkt |

Diagramm mit Ausreißer
Einer der Punkte ist viel größer als alle anderen Punkte. Daher handelt es sich bei dem Punkt um einen Ausreißer. Wenn zu viele Ausreißer auftreten, ist das Modell möglicherweise nicht akzeptabel. Versuchen Sie nach Möglichkeit, die Ursache von Ausreißern zu ermitteln. Korrigieren Sie sämtliche Dateneingabe- oder Messfehler. Erwägen Sie, Datenwerte zu entfernen, die auf ungewöhnliche, einmalige Ereignisse (Ausnahmebedingungen) zurückzuführen sind. Wiederholen Sie anschließend die Analyse.
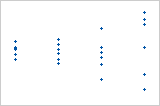
Diagramm mit nicht konstanter Varianz
Die Varianz der Residuen nimmt mit den angepassten Werten zu. Beachten Sie, dass sich bei zunehmenden Werten der Anpassungen die Streuung der Residuen verbreitert. Dieses Muster weist darauf hin, dass die Varianzen der Residuen ungleich (nicht konstant) sind.
Residuen vs. Reihenfolge
Das Diagramm der Residuen im Vergleich zur Reihenfolge zeigt die Residuen in der Reihenfolge an, in der die Daten erfasst wurden.
Interpretation
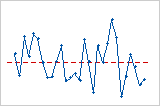
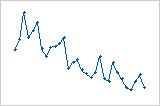
Trend
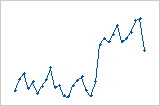
Shift
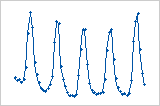
Zyklus
Residuen vs. Variablen
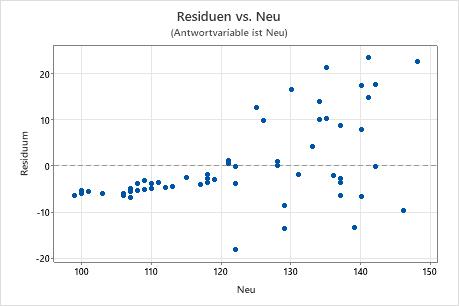
Das Diagramm der Residuen im Vergleich zu den Variablen veranschaulicht die Residuen im Vergleich zu einer anderen Variablen. Die Variable kann bereits im Modell enthalten sein. Es ist auch möglich, dass die Variable nicht im Modell enthalten ist, und Sie vermuten, dass sie die Antwortvariable beeinflusst.
Interpretation
Die orthogonale Regression wird oft in der klinischen Chemie oder in Laboratorien verwendet, um zu untersuchen, ob zwei Instrumente oder Methoden gleich messen. Muster in einem Diagramm der Residuen im Vergleich zu der Antwortvariablen bzw. Prädiktorvariablen können Auskunft darüber geben, inwiefern sich die Methoden voneinander unterscheiden.
In diesen Ergebnissen weist das Diagramm der Residuen im Vergleich zu den Anpassungen ein Muster auf, bei dem sich alle hohen Residuen in der Mitte des Diagramms befinden. Ein Diagramm der Residuen im Vergleich zu der Antwortvariablen zeigt, dass die Übereinstimmung mit der anderen Methode abnimmt, je größer die Messwerte für die neue Methode werden.