Methoden in Nichtlineare Regression

Die Modellfunktion für Beobachtung n wird wie folgt angegeben:

Minitab betrachtet die Modellfunktion für alle N Beobachtungen als vektorwertige Funktion der Parameter:

ein (N X 1)-Vektor mit den Elementen .

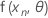
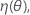
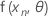Die Jacobi-Matrix von η ist eine (N X P)-Matrix mit Elementen, die gleich den partiellen Ableitungen der Modellfunktion in Bezug auf die Parameter sind:

Sei Vⁱ = V(θⁱ) die Jacobi-Matrix, ausgewertet bei θⁱ, dem Parameterschätzwert nach der i-ten Iteration.

Dann ist eine lineare Approximation für η:

was die Grundlage für die Gauß-Newton-Methode und für näherungsweise Rückschlüsse bildet.

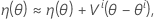
Sei θ* der Schätzwert der kleinsten Quadrate.

Standardmäßig verwendet Minitab die Gauß-Newton-Methode zum Ermitteln des Schätzwerts der kleinsten Quadrate. Die Methode verwendet eine lineare Approximation an die Modellfunktion, um einen anfänglichen Schätzwert von θ⁰ für θ iterativ zu verbessern. Anschließend verbessert die Methode die Schätzwerte weiter, bis der relative Versatz unterhalb der vorgeschriebenen Toleranz¹ liegt. Das heißt, Minitab erweitert die Modellfunktion f(x_n,θ) in einer Taylorreihe erster Ordnung um θ⁰ wie folgt:

Dabei gilt Folgendes:

mit p = 1, 2,..., p

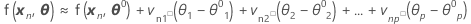
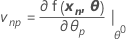
Einschließlich aller N Fälle

Hierbei ist V⁰ die NxP-Derivatmatrix mit den Elementen {v_np}. Dies entspricht der Approximation der Residuen z(θ) = y – η(θ) als:

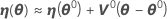
Dabei gilt Folgendes:

und

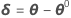
Minitab berechnet das Gauß-Inkrement δ⁰ zum Minimieren der ungefähren Summe der Quadrate der Residuen 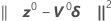unter Verwendung von:

und somit: .

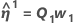
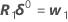Der Punkt

sollte jetzt näher an y als η(θ⁰) sein, und Minitab verwendet den Wert θ¹ = θ⁰ + δ⁰ zum Durchführen einer weiteren Iteration, indem neue Residuen z¹ = y – η(θ¹), eine neue Derivatmatrix V¹ und ein neues Inkrement berechnet werden. Minitab wiederholt diesen Vorgang bis zur Konvergenz, die erreicht ist, wenn das Inkrement so klein ist, dass es keine sinnvolle Änderung der Elemente des Parametervektors gibt.

Manchmal führt das Gauß-Newton-Inkrement zu einer Zunahme bei der Summe der Quadrate. In diesem Fall ist die lineare Approximation dennoch eine nahe Approximation an die tatsächliche Oberfläche für einen hinreichend kleinen Bereich um η(θ⁰). Um die Summe der Quadrate zu verringern, bindet Minitab den Schrittfaktor λ ein und berechnet Folgendes:

Minitab beginnt mit λ = 1 und dividiert diesen Wert durch zwei, bis S(θ¹) < S( θ⁰).

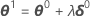
1. Bates und Watts (1988). Nonlinear Regression Analysis and Its Applications. John Wiley & Sons, Inc.

Wenn die Spalten in der Gradientenmatrix V Kollinearität aufweisen, kann diese singulär werden und damit zu Sprüngen bei den Gauß-Newton-Iterationen führen. Um die Singularität zu beherrschen, kann Minitab das Gauß-Newton-Inkrement in den Levenberg-Kompromiss ändern:

Alternativ kann er auch in den Marquardt-Kompromiss geändert werden:

Hierbei ist k ein Konditionierungsfaktor und D eine Diagonalmatrix mit Einträgen, die gleich den Diagonalelementen von V^TV sind. Die Richtung von δ(k) liegt zwischen der Richtung des Gauß-Newton-Inkrements (k → 0) und der Richtung des steilsten Abstiegs:

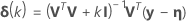
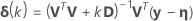
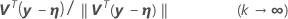.¹

1. Bates and Watts (1988). Nonlinear Regression Analysis and Its Applications. John Wiley & Sons, Inc.

Standardmäßig stellt Minitab die Konvergenz fest, wenn der relative Versatz kleiner als 1,0e-5 ist. Damit wird sichergestellt, dass sich die Tatsache, dass der aktuelle Parametervektor weniger als 0,001 % des Radius des Konfidenzbereichskreises vom Punkt der kleinsten Quadrate entfernt ist, nicht wesentlich auf die Rückschlüsse auswirkt.¹

1. Bates und Watts (1988). Nonlinear Regression Analysis and Its Applications. John Wiley & Sons, Inc.