In diesem Thema
Darstellung der Anpassungslinie
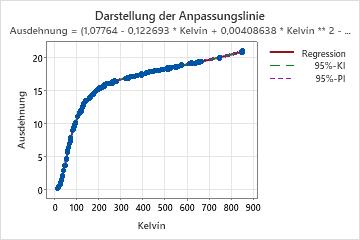
Wenn das nichtlineare Modell einen Prädiktor enthält, zeigt Minitab die Darstellung der Anpassungslinie an, in der die Beziehung zwischen der Antwortvariablen und den Prädiktordaten veranschaulicht wird. Die Darstellung enthält die Regressionslinie, die die Regressionsgleichung abbildet. Sie können auch angeben, dass in der Darstellung das 95%-Konfidenzintervall und das 95%-Prognoseintervall angezeigt werden sollen.
Interpretation
- Die Stichprobe enthält eine angemessene Anzahl von Beobachtungen über die gesamte Spannweite aller Prädiktorwerte.
- Das Modell ist an die Krümmung in den Daten angepasst. Um das beste Modell zu ermitteln, untersuchen Sie das Diagramm, den Standardfehler der Regression (S) sowie den Test auf fehlende Anpassung, wenn die Daten Replikationen enthalten.
- Suchen Sie nach Ausreißern, die einen starken Einfluss auf die Ergebnisse ausüben können. Versuchen Sie, die Ursache von Ausreißern zu ermitteln. Korrigieren Sie sämtliche Dateneingabe- oder Messfehler. Erwägen Sie, Datenwerte zu entfernen, die auf ungewöhnliche, einmalige Ereignisse (Ausnahmebedingungen) zurückzuführen sind. Wiederholen Sie anschließend die Analyse. Weitere Informationen zum Erkennen von Ausreißern finden Sie unter Ungewöhnliche Beobachtungen.
Gleichung
Verwenden Sie die Regressionsgleichung, um die Beziehung zwischen der Antwortvariablen und den Termen im Modell zu beschreiben. Die Regressionsgleichung ist eine algebraische Darstellung der Regressionslinie. Geben Sie den Wert jedes Prädiktors in die Gleichung ein, um den Mittelwert der Antwortvariablen zu berechnen. Im Gegensatz zur linearen Regression kann eine Gleichung für die nichtlineare Regression viele verschiedene Formen annehmen.
Bei nichtlinearen Gleichungen ist es häufig weniger intuitiv als bei linearen Gleichungen, die Effekte der einzelnen Prädiktoren auf die Antwortvariable zu ermitteln. Anders als bei den Parameterschätzwerten in linearen Modellen gibt es für Parameterschätzwerte in nichtlinearen Modellen keine einheitliche Interpretation. Die korrekte Interpretation für jeden Parameter hängt von der Modellfunktion und der Position des Parameters in der Formel ab. Wenn das nichtlineare Modell nur einen Prädiktor enthält, untersuchen Sie die Darstellung der Anpassungslinie, um die Beziehung zwischen dem Prädiktor und der Antwortvariablen zu erkennen.
Die Konvergenz gegen eine Lösung bedeutet nicht notwendigerweise eine optimale Anpassung des Modells oder eine minimale Summe der quadrierten Fehler (SSE). Aufgrund eines lokalen SSE-Minimums oder einer inkorrekten Modellfunktion kann der Algorithmus bei falschen Parameterwerten konvergieren. Daher ist es unerlässlich, die Parameterwerte, die Darstellung der Anpassungslinie und die Residuendiagramme zu untersuchen, um zu ermitteln, ob die Modellanpassung und die Parameterschätzwerte angemessen sind.
Interpretation
In diesen Ergebnissen sind ein Prädiktor und sieben Parameterschätzwerte vorhanden. Die Antwortvariable ist „Ausdehnung“, während die Prädiktorvariable die Temperatur auf der Kelvin-Skala ist. Die umfangreiche Gleichung beschreibt die Beziehung zwischen der Antwortvariablen und den Prädiktoren. Der Effekt, den eine Erhöhung um 1 Grad Kelvin auf die Ausdehnung des Kupfers hat, hängt in hohem Maße vom der Ausgangstemperatur ab. Der Effekt der Temperaturänderungen auf die Kupferausdehnung kann nicht auf einfache Weise zusammengefasst werden. Untersuchen Sie die Darstellung der Anpassungslinie, um die Beziehung zwischen dem Prädiktor und der Antwortvariablen zu erkennen.
Wenn Sie einen Wert für die Temperatur in Kelvin in die Gleichung einsetzen, ist das Ergebnis der angepasste Wert für die Kupferausdehnung.
Gleichung
** 3) / (1 - 0,00576099 * Kelvin + 0,000240537 * Kelvin ** 2 - 1,23144E-07 * Kelvin ** 3)
95%-KI
Das Konfidenzintervall für die Anpassung gibt einen Bereich wahrscheinlicher Werte für den Mittelwert der Antwortvariablen bei bestimmten Einstellungen der Prädiktoren an.
Interpretation
Verwenden Sie das Konfidenzintervall, um den Schätzwert des angepassten Werts für die beobachteten Werte der Variablen auszuwerten.
Bei einem 95%-Konfidenzniveau können Sie sich beispielsweise zu 95 % sicher sein, dass das Konfidenzintervall den Mittelwert der Grundgesamtheit für die angegebenen Werte der Variablen im Modell enthält. Anhand des Konfidenzintervalls können Sie die praktische Signifikanz Ihrer Ergebnisse beurteilen. Bestimmen Sie anhand Ihrer Fachkenntnisse, ob das Konfidenzintervall Werte umfasst, die in der jeweiligen Situation von praktischer Signifikanz sind. Ein breites Konfidenzintervall deutet darauf hin, dass Sie sich bezüglich des Mittelwerts von künftigen Werten weniger sicher sein können. Wenn das Intervall zu breit und damit nicht hilfreich ist, erwägen Sie, den Stichprobenumfang zu vergrößern.
95%-PI
Das Prognoseintervall ist ein Bereich, der bei bestimmten Einstellungen für die Prädiktoren wahrscheinlich einen einzelnen zukünftigen Wert der Antwortvariablen für einen bestimmten Wert der Prädiktorvariablen enthält.
Interpretation
Ein Materialtechniker in einem Möbelwerk entwickelt beispielsweise ein einfaches Regressionsmodell, um die Steife einer Spanplatte anhand der Dichte der Platte zu prognostizieren. Der Techniker vergewissert sich, dass das Modell die Annahmen der Analyse erfüllt. Anschließend verwendet er das Modell zum Prognostizieren der Steife.
Mit der Regressionsgleichung wird prognostiziert, dass die Steife für eine neue Beobachtung 66,995 beträgt und das Prognoseintervall [50; 85] lautet. Es ist zwar unwahrscheinlich, dass die Beobachtung eine Steife von genau 66,995 aufweist. Das Prognoseintervall weist jedoch darauf hin, dass sich der Techniker zu 95 % sicher sein kann, dass der tatsächliche Wert zwischen ungefähr 48 und 86 liegt.
Das Prognoseintervall ist immer breiter als das entsprechende Konfidenzintervall. Dies ist auf die zusätzliche Unsicherheit beim Prognostizieren eines einzelnen Werts der Antwortvariablen gegenüber dem Mittelwert der Antwortvariablen zurückzuführen.
