In diesem Thema
Modell
Minitab berechnet für ein Modell mit K Kategorien der Antwortvariablen K – 1 Logit-Funktionen. Eine Antwortvariable mit drei Kategorien (1, 2, 3) weist z. B. zwei Logit-Funktionen auf (Referenzereignis = 3):
Formel
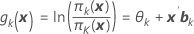
Notation
| Begriff | Beschreibung |
|---|---|
| gk ( x ) | Logit-Linkfunktion |
| θk | mit der k-ten eindeutigen Kategorie der Antwortvariablen verbundene Konstante |
| x k | Vektor der Prädiktorvariablen |
| b k | mit der k-ten Logit-Funktion verbundener Vektor der Koeffizienten |
Faktoren-/Kovariatenmuster
Beschreibt einen einzelnen Satz von Faktoren-/Kovariatenwerten in einem Datensatz. Minitab berechnet für jedes Faktoren-/Kovariatenmuster Ereigniswahrscheinlichkeiten, Residuen und weitere Bewertungsmaße.
Wenn ein Datensatz beispielsweise die Faktoren Geschlecht und Ethnie sowie die Kovariate Alter enthält, können die Kombinationen dieser Prädiktoren so viele verschiedene Kovariatenmuster wie Probanden enthalten. Wenn ein Datensatz nur die Faktoren Ethnie und Geschlecht enthält, die jeweils auf zwei Stufen kodiert sind, gibt es nur vier mögliche Faktoren-/Kovariatenmuster. Wenn Sie die Daten als Häufigkeiten oder als Erfolge, Versuche oder Misserfolge eingeben, enthält jede Zeile ein Faktoren-/Kovariatenmuster.
Ereigniswahrscheinlichkeit
Wird als π bezeichnet. Für ein Modell mit den drei Kategorien 1, 2 und 3 (Referenzereignis 3) betragen die konditionalen Wahrscheinlichkeiten:
Formel
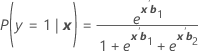
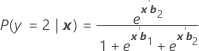
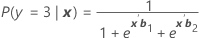
Und die Ereigniswahrscheinlichkeit beträgt:
π k (x) = P(y = k| x ) für k = 1, 2, 3. Jede Wahrscheinlichkeit ist eine Funktion des Vektors von 2(p + 1) Parametern, b ' = ( b '1, b '2)
Log-Likelihood
Die Log-Likelihood-Funktion wird maximiert, um optimale Werte von b zu ermitteln. Für ein Modell mit 3 Kategorien in der Antwortvariablen (Referenz = 3) lautet die Log-Likelihood-Funktion wie folgt:
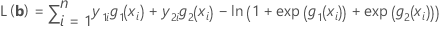
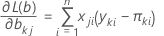
Die Schätzwerte der Maximum-Likelihood werden berechnet, indem diese Gleichungen auf null gesetzt und nach b aufgelöst werden.
Notation
| Begriff | Beschreibung |
|---|---|
| k | 1, 2 |
| j | 0, 1, 2, ..., p |
| p | Anzahl der Koeffizienten im Modell ohne den Koeffizienten für die Konstante |
| πki | πk(xi), mit x0i für jedes Subjekt |
Koeffizienten
Die Schätzwerte der Maximum-Likelihood, auch als Parameterschätzwerte bezeichnet. Wenn K eindeutige Werte der Antwortvariablen vorhanden sind, schätzt Minitab für jeden Prädiktor K – 1 Sätze von Parameterschätzwerten. Die Effekte variieren in Abhängigkeit von der Kategorie der Antwortvariablen im Vergleich zum Referenzereignis. Jeder Logit gibt die geschätzten Differenzen bei den logarithmierten Chancen einer Kategorie der Antwortvariablen im Vergleich zum Referenzereignis an. Die Parameter in den K – 1 Gleichungen bestimmen anhand aller anderen Paare von Kategorien der Antwortvariablen die Parameter für die Logits.
Die geschätzten Koeffizienten werden mit Hilfe einer iterativen Methode der jeweils neu gewichteten kleinsten Quadrate berechnet; dies entspricht der Maximum-Likelihood-Schätzmethode.1,2
Literaturhinweise
- D.W. Hosmer und S. Lemeshow (2000). Applied Logistic Regression. 2nd Ed. John Wiley & Sons, Inc.
- P. McCullagh und J.A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
Standardfehler der Koeffizienten
Asymptotischer Standardfehler, der die Genauigkeit des geschätzten Koeffizienten angibt. Je geringer der Standardfehler ist, desto genauer ist der Schätzwert.
Weitere Informationen finden Sie unter [1] und [2].
- A. Agresti (1990). Categorical Data Analysis. John Wiley & Sons, Inc.
- P. McCullagh und J. A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
Z
Mit Hilfe von z wird ermittelt, ob der Prädiktor eine signifikante Beziehung zur Antwortvariablen aufweist. Größere Absolutwerte von z weisen auf eine signifikante Beziehung hin. Der p-Wert gibt an, wo sich z innerhalb der Normalverteilung befindet.
Formel
z = βi / Standardfehler
Die Formel für die Konstante lautet:
z = θk / Standardfehler
Bei kleinen Stichproben ist der Likelihood-Quotienten-Test möglicherweise zuverlässiger zum Erkennen der Signifikanz.
p-Wert (p)
p-Werte werden in Hypothesentests verwendet, um Ihnen die Entscheidung zu ermöglichen, ob eine Nullhypothese zurückgewiesen oder nicht zurückgewiesen werden sollte. Der p-Wert stellt die Wahrscheinlichkeit dar, eine Teststatistik zu erhalten, die mindestens so extrem wie der tatsächlich berechnete Wert ist, wenn die Nullhypothese wahr ist. Ein häufig verwendeter Trennwert für den p-Wert ist 0,05. Wenn beispielsweise der berechnete p-Wert einer Teststatistik kleiner als 0,05 ist, weisen Sie die Nullhypothese zurück.
Chancenverhältnis
Dies ist nützlich, um die Beziehung zwischen einem Prädiktor und einer Antwortvariablen zu interpretieren.
Das Chancenverhältnis q kann eine beliebige nicht negative Zahl sein. Die Basis für den Vergleich ist ein Chancenverhältnis von 1. Wenn θ = 1, liegt keine Assoziation zwischen der Antwortvariablen und dem Prädiktor vor. Wenn θ > 1, sind die Chancen des Vergleichsereignisses der Antwortvariablen auf der Referenzstufe des Faktors (oder für höhere Stufen eines stetigen Prädiktors) höher. Wenn θ < 1, sind die Chancen des Vergleichsereignisses der Antwortvariablen auf der Referenzstufe des Faktors (oder für höhere Stufen eines stetigen Prädiktors) geringer. Werte, die weiter von 1 entfernt liegen, weisen auf eine stärkere Assoziation hin.
Bei einem Modell mit drei Kategorien von Antwortvariablen (1, 2, 3) und einem Prädiktor gibt das Chancenverhältnis beispielsweise die Chancen für die Ergebniskategorie k im Vergleich zu der als Referenzereignis verwendeten Ergebniskategorie (in diesem Beispiel Kategorie 3) an. Die folgende Formel gilt für das Chancenverhältnis eines Prädiktors mit den zwei Stufen a und b.
Formel
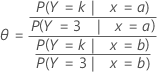
Notation
| Begriff | Beschreibung |
|---|---|
| k | Ergebniskategorie |
Konfidenzintervall
Formel
Das große Stichprobenkonfidenzintervall für βi beträgt:
β i + Zα /2* (Standardfehler)
Um das Konfidenzintervall für das Chancenverhältnis zu erhalten, potenzieren Sie die Unter- und die Obergrenze des Konfidenzintervalls. Das Intervall gibt den Bereich an, in dem die Chance für jede Änderung des Prädiktors um eine Einheit liegen kann.
Notation
| Begriff | Beschreibung |
|---|---|
| α | Signifikanzniveau |
Varianz-Kovarianz-Matrix
Eine Quadratmatrix mit der Größe p +1 × (K – 1). Die Varianz jedes Koeffizienten befindet sich in der Diagonalzelle, und die Kovarianz jedes Koeffizientenpaars befindet sich in der entsprechenden nicht diagonalen Zelle. Die Varianz ist der quadrierte Standardfehler des Koeffizienten.
Die Varianz-Kovarianz-Matrix ist asymptotisch und ergibt sich aus der letzten Iteration der Umkehrung der Informationsmatrix. Die Kovarianzmatrix wird anhand der Matrix der zweiten partiellen Ableitungen ermittelt.
Notation
| Begriff | Beschreibung |
|---|---|
| p | Anzahl der Prädiktoren |
| K | Anzahl der Kategorien in der Antwortvariablen |
Pearson
Hierbei handelt es sich um eine zusammenfassende Statistik auf der Grundlage der Pearson-Residuen, die angibt, wie gut das Modell an die Daten angepasst ist. Der Pearson-Wert ist nicht hilfreich, wenn die Anzahl der eindeutigen Werte der Kovariate annähernd der Anzahl der Beobachtungen entspricht, sie ist jedoch nützlich, wenn wiederholte Beobachtungen auf derselben Kovariatenstufe vorliegen. Höhere χ2-Teststatistiken und niedrigere p-Werte weisen darauf hin, dass das Modell möglicherweise nicht gut an die Daten angepasst ist.
Die Formel lautet:
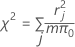
Hierbei ist r = Pearson-Residuum, m = Anzahl der Versuche im j-ten Faktoren-/Kovariatenmuster und π0 = hypothetischer Wert des Anteils.
Abweichung
Hierbei handelt es sich um eine zusammenfassende Statistik auf der Grundlage der Abweichungsresiduen, die angibt, wie gut das Modell an die Daten angepasst ist. Die Abweichung ist nicht hilfreich, wenn die Anzahl der eindeutigen Werte der Kovariate annähernd der Anzahl der Beobachtungen entspricht, sie ist jedoch nützlich, wenn wiederholte Beobachtungen auf derselben Kovariatenstufe vorliegen. Höhere D-Werte und niedrigere p-Werte weisen darauf hin, dass das Modell möglicherweise nicht gut an die Daten angepasst ist. Der Test weist (k – 1)*J − (p) Freiheitsgrade auf, wobei k die Anzahl der Kategorien in der Antwortvariablen, J die Anzahl der eindeutigen Faktoren-/Kovariatenmuster und p die Anzahl der Koeffizienten ist.
Die Formel lautet:
D =2 Σ yik log p ik− 2 Σ yik log π ik
wobei πik = Wahrscheinlichkeit der i-ten Beobachtung für die k-te Kategorie ist.
