In diesem Thema
- Schritt 1: Bestimmen, ob die Assoziation zwischen der Antwortvariablen und dem Term statistisch signifikant ist
- Schritt 2: Bestimmen, ob die Regressionslinie an Ihre Daten angepasst ist
- Schritt 3: Untersuchen der Assoziation zwischen Term und Antwortvariable
- Schritt 4: Bestimmen, wie gut das Modell an die Daten angepasst ist
- Schritt 5: Bestimmen, ob das Modell die Annahmen der Analyse erfüllt
Schritt 1: Bestimmen, ob die Assoziation zwischen der Antwortvariablen und dem Term statistisch signifikant ist
- p-Wert ≤ α: Die Assoziation ist statistisch signifikant
- Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, können Sie schlussfolgern, dass eine statistisch signifikante Assoziation zwischen der Antwortvariablen und dem Term besteht. Wenn Sie ein quadratisches oder ein kubisches Modell anpassen und die quadratischen bzw. kubischen Terme signifikant sind, können Sie schlussfolgern, dass die Daten eine Krümmung aufweisen.
- p-Wert > α: Die Assoziation ist statistisch nicht signifikant
-
Wenn der p-Wert größer als das Signifikanzniveau ist, können Sie nicht schlussfolgern, dass eine statistisch signifikante Assoziation zwischen der Antwortvariablen und dem Term besteht. Wenn Sie ein quadratisches oder ein kubisches Modell anpassen und die quadratischen bzw. kubischen Terme statistisch nicht signifikant sind, empfiehlt es sich möglicherweise, ein anderes Modell auszuwählen.
Varianzanalyse
| Quelle | DF | SS | MS | F | p |
|---|---|---|---|---|---|
| Regression | 2 | 12189,4 | 6094,70 | 106,54 | 0,000 |
| Fehler | 26 | 1487,3 | 57,21 | ||
| Gesamt | 28 | 13676,7 |
Sequenzielle Varianzanalyse
| Quelle | DF | SS | F | p |
|---|---|---|---|---|
| Linear | 1 | 11552,8 | 146,86 | 0,000 |
| Quadratisch | 1 | 636,6 | 11,13 | 0,003 |
Wichtigstes Ergebnis: p-Wert
In diesen Ergebnissen ist der p-Wert für den linearen Term, Dichte, gleich 0,000 und für den quadratischen Term, Dichte 2, gleich 0,003. Beide Werte sind kleiner als das Signifikanzniveau 0,05. Diese Ergebnisse zeigen, dass die Assoziation zwischen Steife und Dichte statistisch relevant ist.
Schritt 2: Bestimmen, ob die Regressionslinie an Ihre Daten angepasst ist
- Die Stichprobe enthält eine angemessene Anzahl von Beobachtungen über die gesamte Spannweite aller Prädiktorwerte.
- Das Modell ist an eine ggf. vorhandene Krümmung in den Daten angepasst. Wenn Sie ein lineares Modell anpassen und eine Krümmung in den Daten feststellen, wiederholen Sie die Analyse, und wählen Sie das quadratische oder kubische Modell aus. Um das beste Modell zu ermitteln, untersuchen Sie das Diagramm sowie die Statistiken für die Güte der Anpassung. Prüfen Sie den p-Wert für die Terme im Modell, um sich zu vergewissern, dass sie statistisch signifikant sind, und bewerten Sie anhand Ihrer Kenntnis des Prozesses die praktische Signifikanz.
- Suchen Sie nach Ausreißern, die einen starken Einfluss auf die Ergebnisse ausüben können. Versuchen Sie, die Ursache von Ausreißern zu ermitteln. Korrigieren Sie sämtliche Dateneingabe- oder Messfehler. Erwägen Sie, Datenwerte zu entfernen, die auf ungewöhnliche, einmalige Ereignisse (Ausnahmebedingungen) zurückzuführen sind. Wiederholen Sie anschließend die Analyse. Weitere Informationen zum Erkennen von Ausreißern finden Sie unter Ungewöhnliche Beobachtungen.
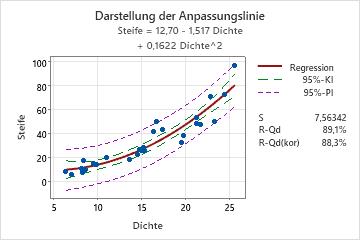
Schritt 3: Untersuchen der Assoziation zwischen Term und Antwortvariable
Wenn der p-Wert des Terms signifikant ist, können Sie die Regressionsgleichung und die Koeffizienten untersuchen, um festzustellen, in welcher Beziehung der Term zur Antwortvariablen steht.
Verwenden Sie die Regressionsgleichung, um die Beziehung zwischen der Antwortvariablen und den Termen im Modell zu beschreiben. Die Regressionsgleichung ist eine algebraische Darstellung der Regressionslinie. Die Regressionsgleichung für das lineare Modell nimmt die folgende Form an: Y= b0 + b1x1. In der Regressionsgleichung steht Y für die Antwortvariable, b0 ist die Konstante bzw. der Schnittpunkt mit der y-Achse, b1 ist der geschätzte Koeffizient für den linearen Term (auch als Steigung der Linie bezeichnet), und x1 steht für den Wert des Terms.
Der Koeffizient des Terms stellt die Änderung des Mittelwerts der Antwortvariablen bei einer Änderung dieses Terms um eine Einheit dar. Das Vorzeichen des Koeffizienten gibt die Richtung der Beziehung zwischen dem Term und der Antwortvariablen an. Wenn der Koeffizient negativ ist, nimmt der Mittelwert der Antwortvariablen bei Zunahme des Terms ab. Wenn der Koeffizient positiv ist, nimmt der Mittelwert der Antwortvariablen bei zunehmendem Term zu.
Ein Manager stellt beispielsweise fest, dass das Ergebnis eines Mitarbeiters in einem Test seiner beruflichen Fähigkeiten mit dem Regressionsmodell y = 130 + 4,3x prognostiziert werden kann. In der Gleichung steht x für die Anzahl der absolvierten Stunden interner Schulung (von 0 bis 20), und y ist das Testergebnis. Der Koeffizient bzw. die Steigung ist 4,3, womit angegeben wird, dass sich das mittlere Testergebnis mit jeder absolvierten Schulungsstunde um 4,3 Punkte erhöht.
Weitere Informationen zu Koeffizienten finden Sie unter Regressionskoeffizienten.
Steife = 12,70 - 1,517 Dichte + 0,1622 Dichte^2
Zusammenfassung des Modells
| S | R-Qd | R-Qd(kor) |
|---|---|---|
| 7,56342 | 89,13% | 88,29% |
Wichtigste Ergebnisse: Regressionsgleichung, Koeffizient
Der Koeffizient für den Prädiktor, Dichte, ist –1,517 und für Dichte2 0,1622. Daher steigt bei einer quadratischen Beziehung die durchschnittliche Steife der Spanplatten schneller bei hohen Dichtewerten als bei niedrigeren Dichtewerten.
Schritt 4: Bestimmen, wie gut das Modell an die Daten angepasst ist
Um zu ermitteln, wie gut das Modell an die Daten angepasst ist, untersuchen Sie die Statistiken für die Güte der Anpassung in der Tabelle „Zusammenfassung des Modells“.
- R-Qd
-
R2 ist der Prozentsatz der Streuung in der Antwortvariablen, der durch das Modell erklärt wird.Je höher das R2, desto besser ist das Modell für Ihre Daten passend.R2 liegt immer zwischen 0 % und 100 %.
Der Wert von R2 nimmt beim Einbinden zusätzlicher Prädiktoren in das Modell stets zu. Das beste Modell mit fünf Prädiktoren weist beispielsweise immer ein R2 auf, das mindestens so hoch wie das des besten Modells mit vier Prädiktoren ist. Daher ist R2 am nützlichsten, wenn Sie Modelle derselben Größe vergleichen.
- R-Qd(kor)
-
Verwenden Sie das korrigierte R2, wenn Sie Modelle vergleichen möchten, die eine unterschiedliche Anzahl von Prädiktoren enthalten. R2 nimmt stets zu, wenn Sie einen zusätzlichen Prädiktor in das Modell aufnehmen, selbst wenn damit keine tatsächliche Verbesserung des Modells verbunden ist. Der Wert des korrigierten R2 berücksichtigt die Anzahl der Prädiktoren im Modell, sodass Ihnen das Auswählen des richtigen Modells erleichtert wird.
-
Kleine Stichproben ermöglichen keinen genauen Schätzwert für die Stärke der Beziehung zwischen der Antwortvariablen und den Prädiktoren. Wenn z. B. das R2 genauer sein muss, sollten Sie einen größeren Stichprobenumfang (im Allgemeinen 40 oder mehr) wählen.
-
Statistiken für die Güte der Anpassung sind nur eines der Maße für die Güte der Anpassung des Modells an die Daten. Selbst wenn ein Modell einen erwünschten Wert aufweist, sollten Sie die Residuendiagramme untersuchen, um sich zu vergewissern, dass das Modell die Modellannahmen erfüllt.
Steife = 12,70 - 1,517 Dichte + 0,1622 Dichte^2
Zusammenfassung des Modells
| S | R-Qd | R-Qd(kor) |
|---|---|---|
| 7,56342 | 89,13% | 88,29% |
Wichtigstes Ergebnis: R-Qd
In diesen Ergebnissen lassen sich mit der Dichte der Spanplatte etwa 89 % der Streuung bei der Steife der Platten erklären. Das R2 gibt an, dass das Modell gut an die Daten angepasst ist.
Schritt 5: Bestimmen, ob das Modell die Annahmen der Analyse erfüllt
Verwenden Sie die Residuendiagramme, um zu ermitteln, ob das Modell angemessen ist und die Annahmen der Analyse erfüllt. Wenn die Annahmen nicht erfüllt werden, ist das Modell u. U. nicht gut an die Daten angepasst, und Sie sollten beim Interpretieren der Ergebnisse vorsichtig sein.
Diagramm der Residuen im Vergleich zu den Anpassungen
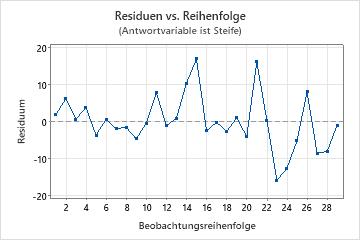
Verwenden Sie das Diagramm der Residuen im Vergleich zu den Anpassungen, um die Annahme zu überprüfen, dass die Residuen zufällig verteilt sind und eine konstante Varianz aufweisen. Im Idealfall sollten die Punkte zufällig auf beiden Seiten von null verteilt sein, und es sollten keine Muster in den Punkten erkennbar sein.
| Muster | Mögliche Bedeutung des Musters |
|---|---|
| Aufgefächerte oder ungleichmäßig gestreute Residuen für die angepassten Werte | Nicht konstante Varianz |
| Krümmung | Ein fehlender Term höherer Ordnung |
| Ein weit von null entfernt liegender Punkt | Ein Ausreißer |
| Ein in x-Richtung weit von den anderen Punkten entfernter Punkt | Ein einflussreicher Punkt |
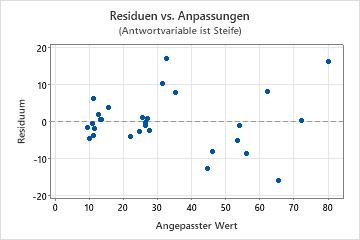
Diagramm der Residuen im Vergleich zur Reihenfolge
Trend
Shift
Zyklus
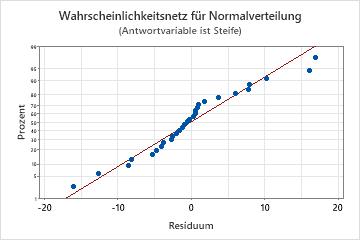
Wahrscheinlichkeitsnetz für Normalverteilung
Verwenden Sie das Wahrscheinlichkeitsnetz (Normal) der Residuen, um die Annahme zu überprüfen, dass die Residuen normalverteilt sind. Die Residuen im Wahrscheinlichkeitsnetz für Normalverteilung sollten ungefähr einer Geraden folgen.
| Muster | Mögliche Bedeutung des Musters |
|---|---|
| Keine Gerade | Nicht-Normalverteilung |
| Ein Punkt weit entfernt von der Linie | Ein Ausreißer |
| Unbeständige Steigung | Eine nicht identifizierte Variable |
Weitere Informationen zum Umgang mit Mustern in den Residuendiagrammen finden Sie unter Residuendiagramme für Darstellung der Anpassungslinie.
