In diesem Thema
Darstellung der Anpassungslinie
In der Darstellung der Anpassungslinie werden die Daten der Antwortvariablen und der Prädiktorvariablen angezeigt. Die Darstellung enthält die Regressionslinie, die die Regressionsgleichung abbildet. Sie können auch angeben, dass in der Darstellung das 95%-Konfidenzintervall und das 95%-Prognoseintervall angezeigt werden sollen.
Interpretation
- Die Stichprobe enthält eine angemessene Anzahl von Beobachtungen über die gesamte Spannweite aller Prädiktorwerte.
- Das Modell ist an eine ggf. vorhandene Krümmung in den Daten angepasst. Wenn Sie ein lineares Modell anpassen und eine Krümmung in den Daten feststellen, wiederholen Sie die Analyse, und wählen Sie das quadratische oder kubische Modell aus. Um das beste Modell zu ermitteln, untersuchen Sie das Diagramm sowie die Statistiken für die Güte der Anpassung. Prüfen Sie den p-Wert für die Terme im Modell, um sich zu vergewissern, dass sie statistisch signifikant sind, und bewerten Sie anhand Ihrer Kenntnis des Prozesses die praktische Signifikanz.
- Suchen Sie nach Ausreißern, die einen starken Einfluss auf die Ergebnisse ausüben können. Versuchen Sie, die Ursache für die Ausreißer zu ermitteln. Korrigieren Sie sämtliche Dateneingabe- oder Messfehler. Erwägen Sie, Datenwerte zu entfernen, die auf ungewöhnliche, einmalige Ereignisse (Ausnahmebedingungen) zurückzuführen sind. Wiederholen Sie anschließend die Analyse. Weitere Informationen zum Erkennen von Ausreißern finden Sie unter Ungewöhnliche Beobachtungen.
Regressionsgleichung
Verwenden Sie die Regressionsgleichung, um die Beziehung zwischen der Antwortvariablen und den Termen im Modell zu beschreiben. Die Regressionsgleichung ist eine algebraische Darstellung der Regressionslinie. Die Regressionsgleichung für das lineare Modell nimmt die folgende Form an: Y = b0 + b1x1. In der Regressionsgleichung steht Y für die Antwortvariable, b0 ist die Konstante bzw. der Schnittpunkt mit der y-Achse, b1 ist der geschätzte Koeffizient für den linearen Term (auch als Steigung der Linie bezeichnet), und x1 steht für den Wert des Terms.
Die Regressionsgleichung mit mehreren Termen weist die folgende Form auf:
y = b0 + b1x1 + b2x2 + ... + bkxk
- y ist die Antwortvariable.
- b0 ist die Konstante.
- b1, b2, ..., bk sind die Koeffizienten.
- x1, x2, ..., xk sind die Werte des Terms.
Koeffizienten der Gleichung
Ein Regressionskoeffizient beschreibt die Größe und Richtung der Beziehung zwischen einem Prädiktor und der Antwortvariablen. Koeffizienten sind die Zahlen, mit denen die Werte des Terms in einer Regressionsgleichung multipliziert werden.
Interpretation
Der Koeffizient des Terms stellt die Änderung des Mittelwerts der Antwortvariablen bei einer Änderung dieses Terms um eine Einheit dar. Das Vorzeichen des Koeffizienten gibt die Richtung der Beziehung zwischen dem Term und der Antwortvariablen an. Wenn der Koeffizient negativ ist, nimmt der Mittelwert der Antwortvariablen bei Zunahme des Terms ab. Wenn der Koeffizient positiv ist, nimmt der Mittelwert der Antwortvariablen bei zunehmendem Term zu.
Ein Manager stellt beispielsweise fest, dass das Ergebnis eines Mitarbeiters in einem Test seiner beruflichen Fähigkeiten mit dem Regressionsmodell y = 130 + 4,3x prognostiziert werden kann. In der Gleichung steht x für die Anzahl der absolvierten Stunden interner Schulung (von 0 bis 20), und y ist das Testergebnis. Der Koeffizient bzw. die Steigung ist 4,3, womit angegeben wird, dass sich das mittlere Testergebnis mit jeder absolvierten Schulungsstunde um 4,3 Punkte erhöht.
Die Größe des Koeffizienten bietet in der Regel einen guten Anhaltspunkt, um die praktische Signifikanz des Effekts eines Terms auf die Antwortvariable zu beurteilen. Die Größe des Koeffizienten liefert jedoch keinen Hinweis darauf, ob ein Term statistisch signifikant ist, da bei den Berechnungen für die Signifikanz auch die Streuung der Daten der Antwortvariablen berücksichtigt wird. Untersuchen Sie den p-Wert für den Term, um die statistische Signifikanz zu ermitteln.
95%-KI
Das Konfidenzintervall für die Anpassung gibt einen Bereich wahrscheinlicher Werte für den Mittelwert der Antwortvariablen bei bestimmten Einstellungen der Prädiktoren an.
Interpretation
Verwenden Sie das Konfidenzintervall, um den Schätzwert des angepassten Werts für die beobachteten Werte der Variablen auszuwerten.
Bei einem 95%-Konfidenzniveau können Sie sich beispielsweise zu 95 % sicher sein, dass das Konfidenzintervall den Mittelwert der Grundgesamtheit für die angegebenen Werte der Variablen im Modell enthält. Anhand des Konfidenzintervalls können Sie die praktische Signifikanz Ihrer Ergebnisse beurteilen. Bestimmen Sie anhand Ihrer Fachkenntnisse, ob das Konfidenzintervall Werte umfasst, die in der jeweiligen Situation von praktischer Signifikanz sind. Ein breites Konfidenzintervall deutet darauf hin, dass Sie sich bezüglich des Mittelwerts von künftigen Werten weniger sicher sein können. Wenn das Intervall zu breit und damit nicht hilfreich ist, erwägen Sie, den Stichprobenumfang zu vergrößern.
95%-PI
Das Prognoseintervall ist ein Bereich, der wahrscheinlich einen einzelnen zukünftigen Wert der Antwortvariablen für einen bestimmten Wert der Prädiktorvariablen enthält.
Interpretation
Bei 95%-Prognosebändern können Sie sich zu 95 % sicher sein, dass neue Beobachtungen in dem Intervall liegen, das durch die violetten Linien markiert wird. (Beachten Sie jedoch, dass dies nur für Dichtewerte gilt, die sich in der Spannweite befinden, die bei der Analyse berücksichtigt wird.)
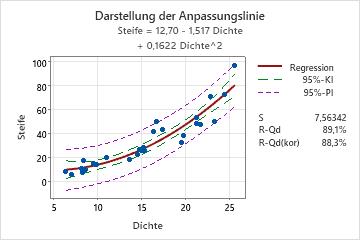
Ein Materialtechniker in einem Möbelwerk entwickelt beispielsweise ein einfaches Regressionsmodell, um die Steife einer Spanplatte anhand der Dichte der Platte zu prognostizieren. Der Techniker vergewissert sich, dass das Modell die Annahmen der Analyse erfüllt. Anschließend verwendet er das Modell zum Prognostizieren der Steife.
Die Regressionsgleichung prognostiziert, dass die Steife für eine neue Beobachtung mit einer Dichte von 20 gleich 12,70 – 1,517*20 + 0,1622*202 oder 47,24 ist. Obwohl es unwahrscheinlich ist, dass eine solche Beobachtung eine Steife von exakt 47,24 aufweist, gibt das Prognoseintervall an, dass sich der Techniker zu 95 % sicher sein kann, dass der tatsächliche Wert ungefähr zwischen 31 und 63 liegt.
Das Prognoseintervall ist immer breiter als das entsprechende Konfidenzintervall. In diesem Beispiel gibt das 95%-Konfidenzintervall an, dass sich der Techniker zu 95 % sicher sein kann, dass die mittlere Steife zwischen ungefähr 43 und 50 liegt.
