Ein Werkstofftechniker in einem Möbelwerk möchte die Steife der vom Unternehmen verbauten Spanplatten untersuchen. Er misst die Steife und die Dichte einer Stichprobe aus Abschnitten von Spanplatten.
Der Techniker bestimmt anhand der einfachen Regression, ob die Dichte der Späne mit der Steife der Platte verknüpft ist.
- Öffnen Sie die Beispieldaten Spanplatte.MWX.
- Wählen Sie aus.
- Geben Sie im Feld Antwort die Spalte Steife ein.
- Geben Sie im Feld Prädiktor die Spalte Dichte ein.
- Wählen Sie unter Typ des Regressionsmodells die Option Quadratisch aus.
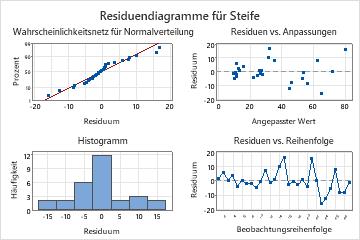
- Klicken Sie auf Grafiken. Wählen Sie unter Residuendiagramme die Option Vier-in-Eins aus. Klicken Sie auf OK.
- Klicken Sie auf Optionen. Wählen Sie unter Darstellungsoptionen die Optionen Konfidenzintervall anzeigen und Prognoseintervall anzeigen aus.
- Klicken Sie in den einzelnen Dialogfeldern auf OK.
Interpretieren der Ergebnisse
In der Tabelle der Varianzanalyse beträgt der p-Wert für das Regressionsmodell 0,000, was bedeutet, dass der tatsächliche p-Wert kleiner als 0,0005 ist. Da der p-Wert kleiner als das Signifikanzniveau 0,05 ist, kann der Techniker schlussfolgern, dass die Assoziation zwischen Steife und Dichte statistisch signifikant ist. In der Tabelle der sequenziellen Varianzanalyse ist der p-Wert für den linearen Term, Dichte, gleich 0,000 und für den quadratischen Term, Dichte 2, gleich 0,003. Beide Werte sind kleiner als das Signifikanzniveau 0,05.
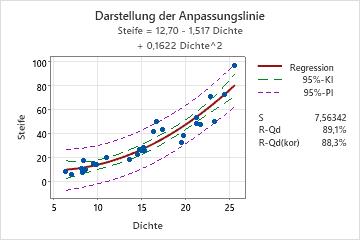
In der rechten oberen Ecke der Darstellung der Anpassungslinie scheint jedoch ein Ausreißer vorhanden zu sein. Da der Ausreißer einen starken Effekt auf die Ergebnisse haben könnte, sollte der Techniker diesen Punkt untersuchen, um seine Ursache zu ermitteln.
Steife = 12,70 - 1,517 Dichte + 0,1622 Dichte^2
Zusammenfassung des Modells
| S | R-Qd | R-Qd(kor) |
|---|---|---|
| 7,56342 | 89,13% | 88,29% |
Varianzanalyse
| Quelle | DF | SS | MS | F | p |
|---|---|---|---|---|---|
| Regression | 2 | 12189,4 | 6094,70 | 106,54 | 0,000 |
| Fehler | 26 | 1487,3 | 57,21 | ||
| Gesamt | 28 | 13676,7 |
Sequenzielle Varianzanalyse
| Quelle | DF | SS | F | p |
|---|---|---|---|---|
| Linear | 1 | 11552,8 | 146,86 | 0,000 |
| Quadratisch | 1 | 636,6 | 11,13 | 0,003 |