In diesem Thema
Gewichtete Regression
Bei der Regression der gewichteten kleinsten Quadrate handelt es sich um eine Methode zum Behandeln von Beobachtungen, deren Varianzen nicht konstant sind. Wenn die Varianzen nicht konstant sind, gelten für die Beobachtungen folgende Hinweise:
- Großen Varianzen sollten relativ kleine Gewichtungen zugewiesen werden.
- Kleinen Varianzen sollten relativ große Gewichtungen zugewiesen werden.
Üblicherweise wird für die Gewichtungen die Umkehrung der reinen Fehlervarianz in der Antwortvariablen ausgewählt.
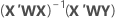
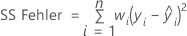
Notation
| Begriff | Beschreibung |
|---|---|
| X | Designmatrix |
| X' | transponierte Designmatrix |
| W | eine (n x n)-Matrix mit den Gewichtungen auf der Diagonalen |
| Y | Vektor von Werten der Antwortvariablen |
| n | Anzahl der Beobachtungen |
| wi | Gewichtung für die i-te Beobachtung |
| yi | Wert der Antwortvariablen für die i-te Beobachtung |
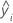 | angepasster Wert für die i-te Beobachtung |
Box-Cox-Transformation
Bei der Box-Cox-Transformation werden Lambda-Werte (siehe unten) ausgewählt, die die Summe der Quadrate der Residuen minimieren. Die resultierende Transformation ist Y λ, wenn λ ≠ 0, und ln(Y), wenn λ = 0. Wenn λ < 0, multipliziert Minitab zudem die transformierte Antwortvariable mit −1, um die Reihenfolge aus der nicht transformierten Antwortvariablen beizubehalten.
Minitab sucht einen optimalen Wert zwischen −2 und 2. Werte, die außerhalb dieses Intervalls liegen, führen möglicherweise nicht zu einer besseren Anpassung.
Hier finden Sie einige der gängigsten Transformationen, wobei Y′ das transformierte Y der Daten darstellt:
| Lambda-Wert (λ) | Transformation |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0,5 | Y′ = 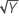 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0,5 |  |
| λ = −1 | Y′ = −1 / Y |
Regressionsgleichung
Für ein Modell mit mehreren Prädiktoren lautet die Gleichung:
y= β0 + β1x1 + ... + βkxk + ε
Die angepasste Gleichung lautet:
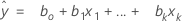
Bei der einfachen linearen Regression, die nur einen Prädiktor enthält, lautet das Modell:
y=ß0+ ß1x1+ε
Mit Regressionsabschätzungen b0 für ß0und b1 für ß1ergibt sich die angepasste Gleichung:
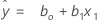
Gleichungen mit einer kategorialen Variablen
- Separate Gleichung jeder Menge kategorischer Prädiktorstufen
- Einzelne Gleichung
- C1
- Die Antwortvariable
- C2
- Ein stetiger Prädiktor
- C3
- Eine kategorische Prädiktorvariable mit den Stufen Rot und Blau
- Blau: C1 = 0,184 + 0,1964*C2
- Rot: C1 = 0,011 + 0,1964*C2
Eine einzelne Gleichung verwendet eine Indikatorvariable, um die kategoriale Variable darzustellen.
C1 = 0,184 + 0,1964*C2 + 0,0*C3_Blau- 0,173*C3_Rot
- Blaue Beobachtung (C3_Blau = 1, C3_Rot = 0): C1 = 0,184 + 0,1964*C2 + 0,0*1 - 0,173*0 = 0,184 + 0,1964*C2
- Rote Beobachtung (C3_Blau = 0, C3_Rot = 1: C1 = 0,084 + 0,1964*C2 + 0,0*0 - 0,173*1 = 0,011 + 0,1964*C2
Notation
| Begriff | Beschreibung |
|---|---|
| y | Antwortvariable |
| xk | K-te Trimester. Jeder Term kann ein einzelner Prädiktor, ein Polynomialterm oder ein Wechselwirkungsterm sein. |
| ßk | k-te Populationsregressionskoeffizient |
| ε | Fehlerterm, der einer Normalverteilung mit dem Mittelwert 0 folgt |
| bk | Schätzung des k-ten Populationsregressionskoeffizienten |
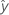 | angepasste Antwortvariable |
Designmatrix
Die Designmatrix enthält die Prädiktoren in einer Matrix (X) mit n Zeilen, wobei n die Anzahl der Beobachtungen ist. Für jeden Koeffizienten im Modell ist eine Spalte vorhanden.
Kategoriale Prädiktoren werden entweder mit der (1; 0)- oder der (-1; 0; 1)-Kodierung kodiert. X enthält keine Spalte für die Referenzstufe des Faktors.
Um die Spalten für einen Wechselwirkungsterm zu berechnen, multiplizieren Sie alle entsprechenden Werte für die Prädiktoren in der Wechselwirkung. Angenommen, die erste Beobachtung weist den Wert 4 für Prädiktor A und den Wert 2 für Prädiktor B auf. In der Designmatrix wird die Wechselwirkung zwischen A und B als 8 (4 x 2) dargestellt.
X'X invers
So entfernt Minitab stark korrelierte Prädiktoren aus der Regressionsgleichung in Regressionsmodell anpassen
Sei rij das Element in der aktuellen mit der SWEEP-Methode behandelten Matrix, das xi und xj zugeordnet ist.
Variablen werden einzeln aufgenommen bzw. entfernt. xk kommt für die Aufnahme in Frage, wenn es sich um eine unabhängige Variable handelt, die aktuell nicht im Modell enthalten ist und bei der rkk ≥ 1 ist (Toleranz mit einem Standardwert von 0,0001) und bei der außerdem für jede Variable xj, die sich aktuell im Modell befindet, Folgendes gilt:
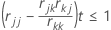
- Minitab wendet die SWEEP-Methode auf die Korrelationsmatrix R an und behandelt x1 … xp dabei wie Zufallsvariablen.
- Für stetige Prädiktoren vergleicht Minitab das Element rkk mit der Toleranz; rkk ≥ Toleranz, wobei k = 1 bis p.
- Für jede aktuell im Modell enthaltene Variable xj prüft Minitab, ob (rjj – rjk * (rkj / rkk)) * Toleranz ≤ 1 ist.
Hinweis
Hierbei sind rkk, rjk, rjj die entsprechenden diagonalen und nicht diagonalen Elemente für die Variablen xj und xk nach Ausführung der SWEEP-Operationen für k Schritte.
- Anderenfalls besteht der Prädiktor den Test nicht und wird aus dem Modell entfernt.
Hinweis
Der Standardwert für die Toleranz ist 8,8e–12.
Hinweis
Sie können den Unterbefehl TOLERANCE mit dem Sessionbefehl REGRESS verwenden, um zu erzwingen, dass Minitab einen Prädiktor im Modell beibehält, der stark mit einem anderen Prädiktor korreliert. Das Absenken der Toleranz ist jedoch nicht ohne Risiko, da so möglicherweise numerisch ungenaue Ergebnisse entstehen.
