Methoden und Formeln für Statistiken für die Güte der Anpassung in Regressionsmodell anpassen

Wählen Sie die gewünschte Methode oder Formel aus.

In diesem Thema

S
R-Qd
R-Qd(kor)
R-Qd (prog)
PRESS
S für Test
R-Qd für Test
S für K Faltungen
R-Qd für K Faltungen
R-Qd für K Faltungen mit schrittweiser Methode
Log-Likelihood
Akaikes korrigiertes Informationskriterium (AICc)
Bayessches Informationskriterium (BIC)
Mallows-Cp

S

Notation

Begriff	Beschreibung
MSE	Mittleres Fehlerquadrat

R-Qd

R² wird auch als Determinationskoeffizient bezeichnet.

Formel

Notation

Begriff	Beschreibung
y_i	i-ter beobachteter Wert der Antwortvariablen
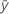	Mittelwert der Antwortvariablen
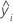	i-ter angepasster Wert der Antwortvariablen

R-Qd(kor)

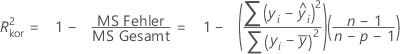
Obwohl die Berechnungen für das korrigierte R² negative Werte ergeben können, zeigt Minitab in derartigen Fällen null an.

Notation

Begriff	Beschreibung
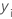	i-ter beobachteter Wert der Antwortvariablen
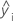	i-ter angepasster Wert der Antwortvariablen
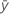	Mittelwert der Antwortvariablen
n	Anzahl der Beobachtungen
p	Anzahl der Terme im Modell

R-Qd (prog)

Obwohl die Berechnungen für R² (prog) negative Werte ergeben können, zeigt Minitab in derartigen Fällen null an.

Notation

Begriff	Beschreibung
y_i	i-ter beobachteter Wert der Antwortvariablen
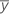	Mittelwert der Antwortvariablen
n	Anzahl der Beobachtungen
e_i	i-tes Residuum
h_i	i-tes Diagonalelement von X(X'X)^–1X'
X	Designmatrix

PRESS

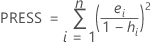
Bewertet die Prognosefähigkeiten des Modells und wird wie folgt berechnet:

Notation

Begriff

Beschreibung

Anzahl der Beobachtungen

e_i

i-tes Residuum

h_i

i-tes Diagonalelement von

X (X' X)^-1X'

S für Test

Das S für den Test fasst den Abstand zwischen den Datenwerten und den angepassten Werten im Testdatensatz zusammen. Das S für den Test wird in den Einheiten der Antwortvariablen gemessen.

Formel

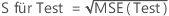
Dabei gilt Folgendes:

Für die Regression

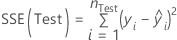
und für die gewichtete Regression

Notation

Begriff	Beschreibung
	Anzahl der Zeilen im Testdatensatz
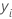	i-ter beobachteter Wert der Antwortvariablen im Testdatensatz
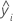	i-ter angepasster Wert der Antwortvariablen im Testdatensatz
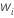	Gewichtung für die i-te Beobachtung im Testdatensatz

R-Qd für Test

Das R² für den Test ist der Prozentsatz der Streuung in der Antwortvariablen des Testdatensatzes, der durch das Modell erklärt wird. Das R² für den Test kann Werte von 0 % bis 100 % annehmen. (Die Berechnungen für das R² für den Test können zwar negative Werte ergeben, die Minitab Statistical Software zeigt jedoch für diese Fälle 0 an.)

Formel

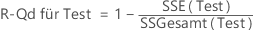
Dabei gilt Folgendes für die Regression

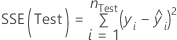
und für die gewichtete Regression

Die Formel für die Gesamtsumme der Quadrate hängt auch davon ab, ob die Daten Gewichtungen enthalten. Für die Regression

und für die gewichtete Regression

Dabei gilt Folgendes:

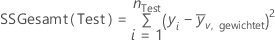
Notation

Begriff	Beschreibung
	Anzahl der Zeilen im Testdatensatz
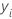	i-ter beobachteter Wert der Antwortvariablen im Testdatensatz
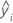	i-ter angepasster Wert der Antwortvariablen im Testdatensatz
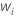	Gewichtung für die i-te Beobachtung im Testdatensatz
	Mittelwert der Antwortvariablen für den Testdatensatz
	gewichteter Mittelwert der Antwortvariablen für den Testdatensatz

S für K Faltungen

Das S für K Faltungen fasst den Abstand zwischen den Datenwerten und den angepassten Werten im Testdatensatz zusammen. Das S für K Faltungen wird in den Einheiten der Antwortvariablen gemessen.

Formel

Dabei gilt Folgendes:

Für die Regression

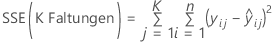
und für die gewichtete Regression

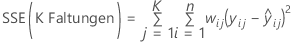Notation

Begriff	Beschreibung
	Anzahl der Zeilen in Faltung j
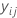	i-ter beobachteter Wert der Antwortvariablen in Faltung j
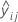	i-ter kreuzvalidierter angepasster Wert der Antwortvariablen in Faltung j
K	Anzahl der Faltungen
w_i	Gewichtung für die i-te Beobachtung in Faltung j

R-Qd für K Faltungen

Das R² für K Faltungen ist der Prozentsatz der Streuung in der Antwortvariablen der Datenfaltungen, der durch das Modell erklärt wird. Das R² für K Faltungen kann Werte von 0 % bis 100 % annehmen. (Die Berechnungen für das R² für K Faltungen können zwar negative Werte ergeben, die Minitab Statistical Software zeigt jedoch für diese Fälle 0 an.)

Formel

Minitab berechnet die Summe der Quadrate für Fehler für jede Faltung. Bei diesen Berechnungen werden für jede Faltung die gleichen Modellterme verwendet; die Schätzungen der Koeffizienten können sich jedoch unterscheiden. Zum Berechnen des R² für K Faltungen werden die Summen der Quadrate für Fehler aus den verschiedenen Faltungen summiert. Für die Regression

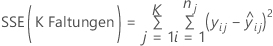
und für die gewichtete Regression

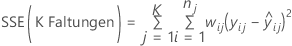Die folgende Formel gibt die Gleichung für das R² für K Faltungen an:

Notation

Begriff	Beschreibung
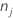	Anzahl der Zeilen ohne fehlende Werte für die Antwortvariable oder fehlende Werte für die Prädiktoren, die die potenziellen Terme im Modell bilden
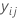	i-ter beobachteter Wert der Antwortvariablen in Faltung j
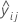	i-ter kreuzvalidierter angepasster Wert der Antwortvariablen in Faltung j
K	Anzahl der Faltungen
w_ij	Gewichtung für die i-te Beobachtung in Faltung j
SSGesamt	Gesamtsumme der Quadrate für alle Daten

R-Qd für K Faltungen mit schrittweiser Methode

Das R-Qd für K Faltungen mit schrittweiser Methode wertet die Anzahl der Terme in einem Modell aus einer Reihe von potenziellen Termen aus. Minitab zeigt negative Werte für das R-Qd für K Faltungen mit schrittweiser Methode an, wenn sie auftreten.

Formel

Minitab berechnet das R-Qd für K Faltungen mit schrittweiser Methode, wenn als schrittweise Auswahlmethode die Vorwärtsauswahl mit Validierung und als Validierungsmethode die Kreuzvalidierung mit K Faltungen ausgewählt ist. Minitab führt die Vorwärtsauswahl K Mal durch, wobei die Daten für jede Faltung einmal ausgelassen werden. Das Modell kann für jede Faltung unterschiedlich sein. Sobald die Verfahren der Vorwärtsauswahl abgeschlossen sind, summiert Minitab die quadrierten Fehler für alle Faltungen in jedem Schritt. Minitab berechnet mit dieser Summe das R-Qd für K Faltungen mit schrittweiser Methode. Für die Regression:

und für die gewichtete Regression:

Anschließend liefert die folgende Formel den Wert des R² für K Faltungen mit schrittweiser Methode für einen Schritt.

Notation

Begriff	Beschreibung
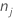	Anzahl der Zeilen ohne fehlende Werte für die Antwortvariable oder fehlende Werte für die Prädiktoren, die die potenziellen Terme im Modell bilden
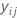	i-ter beobachteter Wert der Antwortvariablen in Faltung j
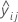	i-ter kreuzvalidierter angepasster Wert der Antwortvariablen in Faltung j
K	Anzahl der Faltungen
w_ij	Gewichtung für die i-te Beobachtung in Faltung j
SSGesamt	Gesamtsumme der Quadrate für alle Daten

Log-Likelihood

Minitab verwendet für nicht gewichtete Analysen folgende Gleichung:

Für Analysen, bei denen die Beobachtungen gewichtet werden, verwendet Minitab die folgende Gleichung:

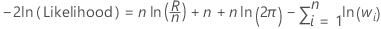
Beobachtungen mit einer Gewichtung von 0 sind in der Analyse nicht enthalten.

Notation

Begriff	Beschreibung
n	Anzahl der Beobachtungen
R	Summe der Quadrate für Fehler für das Modell
w_i	Gewichtung für die i-te Beobachtung

Akaikes korrigiertes Informationskriterium (AICc)

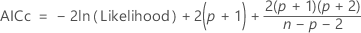
Das AICc wird nicht berechnet, wenn .

Notation

Begriff	Beschreibung
n	Anzahl der Beobachtungen
p	Anzahl der Koeffizienten im Modell einschließlich der Konstante

Bayessches Informationskriterium (BIC)

Notation

Begriff	Beschreibung
p	Anzahl der Koeffizienten im Modell einschließlich der Konstante
n	Anzahl der Beobachtungen

Mallows-Cp

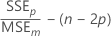
Notation

Begriff	Beschreibung
SSE_p	Summe der quadrierten Fehler für das untersuchte Modell
MSE_m	mittleres Fehlerquadrat für das Modell mit allen potenziellen Termen
n	Anzahl der Beobachtungen
p	Anzahl der Terme im Modell, einschließlich der Konstanten