Methoden und Formeln für Anpassungen und Residuen in Regressionsmodell anpassen

Wählen Sie die gewünschte Methode oder Formel aus.

In diesem Thema

Anpassung
Standardfehler des angepassten Werts (SE Anpassung)
Konfidenzintervall für einen angepassten Wert (KI)
Residuen
Standardisiertes Residuum (Std. Resid)
Standardisiertes Residuum (Std. Resid) mit Validierung
Entfernte (studentisierte) Residuen

Anpassung

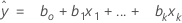
Notation

Begriff	Beschreibung
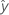	angepasster Wert
x_k	k-ter Term. Jeder Term kann ein einzelner Prädiktor, ein Polynomialterm oder ein Wechselwirkungsterm sein.
b_k	Schätzwert des k-ten Regressionskoeffizienten

Standardfehler des angepassten Werts (SE Anpassung)

Der Standardfehler des angepassten Werts in einem Regressionsmodell mit einem Prädiktor wird wie folgt ausgedrückt:

Der Standardfehler des angepassten Werts in einem Regressionsmodell mit mehreren Prädiktoren wird wie folgt ausgedrückt:

Fügen Sie für die gewichtete Regression die Gewichtsmatrix in die Gleichung ein:

Wenn die Daten über einen Testdatensatz oder eine K-Falten-Kreuzvalidierung verfügen, sind die Formeln identisch. Der Wert von s² stammt aus den Trainingsdaten. Die Designmatrix und die Gewichtsmatrix stammen ebenfalls aus den Trainingsdaten.

Notation

Begriff	Beschreibung
s²	mean square error
n	number of observations
x₀	new value of the predictor
	mean of the predictor
x_i	i^-ter predictor value
x₀	vector of values that produce the fitted values, one for each column in the design matrix, beginning with a 1 for the constant term
X =₀	transpose of the new vector of predictor values
X	design matrix
W	weight matrix

Konfidenzintervall für einen angepassten Wert (KI)

Formel

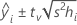
Für die Regression gibt die folgende Formel die Konfidenzgrenzen für einen angepassten Wert an:

Bei der gewichteten Regression enthält die Formel die Gewichtungen:

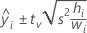
Dabei gilt Folgendes: t_v ist das (1–α/2)-Quantil der t-Verteilung mit v Freiheitsgraden für ein beidseitiges Intervall. Für eine einseitige Grenze ist t_v das (1–α)-Quantil der t-Verteilung mit v Freiheitsgraden.

Wenn Sie einen Testdatensatz oder eine Kreuzvalidierung mit K Faltungen verwenden, stammen die Freiheitsgrade und das mittlere Fehlerquadrat aus dem Trainingsdatensatz.

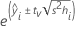
Wenn Sie eine Box-Cox-Transformation ausführen, wenden Sie die inverse Transformation auf die Formel für das Konfidenzintervall an, um die Grenzen in den Einheiten der ursprünglichen Antwortvariablen zu ermitteln. Wenn die Box-Cox-Transformation z. B. der natürliche Logarithmus ist, gibt die folgende Formel die inverse Transformation an:

Notation

Begriff	Beschreibung
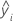	fitted value
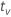	quantile from the t distribution
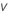	degrees of freedom
	mean square error
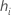	leverage for the i-te observation
w_i	weight for the i-te observation

Residuen

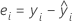
Das Residuum gibt die Differenz zwischen einem beobachteten Wert und dem entsprechenden angepassten Wert an. Dieser Teil der Beobachtung wird nicht durch das Modell erklärt. Das Residuum einer Beobachtung lautet:

Notation

Begriff	Beschreibung
y_i	i-ter beobachteter Wert der Antwortvariablen
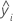	i-ter angepasster Wert der Antwortvariablen

Standardisiertes Residuum (Std. Resid)

Standardisierte Residuen werden auch als intern studentisierte Residuen bezeichnet.

Formel

Notation

Begriff	Beschreibung
e_i	i-tes Residuum
h_i	i-tes Diagonalelement von X(X'X)^–1X'
s²	mittleres Fehlerquadrat
X	Designmatrix
X'	transponierte Designmatrix

Standardisiertes Residuum (Std. Resid) mit Validierung

Bei den Validierungsdaten wird im Nenner der Formel für das standardisierte Residuum die Hebelwirkung addiert und nicht subtrahiert.

Formel

Bei der gewichteten Regression enthält die Formel die Gewichtung:

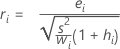
Notation

Begriff	Beschreibung
e_i	i -te residual in the validation data set
h_i	leverage for the i-te validation row
s²	mean square error for the training data set
w_i	weight for the i-te observation in the validation data set

Entfernte (studentisierte) Residuen

Diese werden auch als extern studentisierte Residuen bezeichnet. Die Formel lautet wie folgt:

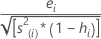
Die Formel kann auch wie folgt ausgedrückt werden:

In dem Modell, mit dem die i-te Beobachtung geschätzt wird, wird die i-te Beobachtung aus dem Datensatz entfernt. Daher kann die i-te Beobachtung den Schätzwert nicht beeinflussen. Jedes entfernte Residuum hat eine Student-t-Verteilung mit 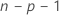Freiheitsgraden.

Notation

Begriff	Beschreibung
e_i	i-tes Residuum
s_(i)²	mittlerer quadrierter Fehler, der ohne die i-te Beobachtung berechnet wurde
h_i	i-tes Diagonalelement von X(X'X)^–1X'
n	Anzahl der Beobachtungen
p	Anzahl der Terme, einschließlich der Konstanten
SSE	Summe der Quadrate für Fehler