Methoden und Formeln für die Regressionsbewertung in Regressionsmodell anpassen

Wählen Sie die gewünschte Methode oder Formel aus.

In diesem Thema

Hebelwirkungen (Hoch)
Hebelwirkungen (hoch) mit Validierung
Cook-Distanz
DFITS
Varianzinflationsfaktor (VIF)
Durbin-Watson-Statistik

Hebelwirkungen (Hoch)

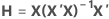
Die Hebelwirkungen werden aus der „Dach-Matrix“ (Hat-Matrix H) berechnet, bei der es sich um eine n x n-Projektionsmatrix handelt:

Die Hebelwirkung der i-ten Beobachtung ist das i-te Diagonalelement h_i von H. Wenn h_i groß ist, weist die i-te Beobachtung ungewöhnliche Prädiktoren (X_1i, X_2i, ..., X_pi) auf. Das heißt, die Prädiktorwerte liegen weit entfernt vom mittleren Vektor 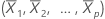, wobei als Maß die Mahalanobis-Distanz verwendet wird.

Hebelwirkungswerte liegen zwischen 0 und 1. Minitab kennzeichnet Beobachtungen mit Hebelwirkungswerten größer als 3p/n oder, falls kleiner, 0,99 in der Tabelle der ungewöhnlichen Beobachtungen mit einem X. Im Allgemeinen sollten Sie Werte mit großen Hebelwirkungen untersuchen.

Notation

Begriff	Beschreibung
X	Versuchsplanmatrix
h_i	i-tes Diagonalelement der „Dach-Matrix“ (Hat-Matrix)
p	Anzahl der Terme im Modell, einschließlich der Konstanten
n	Anzahl der Beobachtungen

Hebelwirkungen (hoch) mit Validierung

Formel

Bei den Validierungsdaten stammen die Hebelwirkungen für jede Zeile aus der folgenden Formel:

Bei der gewichteten Regression enthält die Formel die Gewichtung:

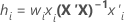
Notation

Begriff	Beschreibung
X	design matrix for the rows in the training data set or the folds that act as the training data set
x_i	the vector of predictors in the i-te validation row
w_i	weight for the i-te validation row

Cook-Distanz

Hierbei handelt es sich um das Gesamtmaß D der kombinierten Auswirkungen aller geschätzten Regressionskoeffizienten auf eine Beobachtung. Minitab berechnet D mit Hebelwirkungswerten und standardisierten Residuen; dabei wird berücksichtigt, ob eine Beobachtung in Bezug auf die x- und y-Werte ungewöhnlich ist. Beobachtungen mit großen D-Werten können Ausreißer sein.

Formel

Die Cook-Distanz ist der Abstand zwischen den Koeffizienten, der mit und ohne die i-te Beobachtung berechnet wurde. Minitab berechnet die Cook-Distanz, ohne dass bei jeder ausgelassenen Beobachtung eine neue Regressionsgleichung angepasst wird. Diese Berechnung lautet wie folgt:

Notation

Begriff	Beschreibung
e_i	i-tes Residuum
h_i	i-tes Diagonalelement von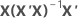
p	Anzahl der Modellparameter, einschließlich der Konstanten
s ²	mittleres Fehlerquadrat
b	Vektor der Koeffizienten
b_(i)	Vektor der Koeffizienten, der nach dem Entfernen der i-ten Beobachtung berechnet wird
X	Versuchsplanmatrix

DFITS

Hiermit werden die Hebelwirkung und das studentisierte Residuum (entfernte t-Residuen) in einem Gesamtmaß zusammengefasst, das ausdrückt, wie ungewöhnlich eine Beobachtung ist. Mit DFITS wird der Einfluss der einzelnen Beobachtungen auf die angepassten Werte in Regressions- und ANOVA-Modellen gemessen. Bei Beobachtungen mit großen DFITS-Werten handelt es sich möglicherweise um Ausreißer.

DFITS stellt die ungefähre Anzahl der Standardabweichungen dar, um die sich der angepasste Wert ändert, wenn je eine Beobachtung aus dem Datensatz entfernt und das Modell erneut angepasst wird. Minitab kann den DFITS-Wert berechnen, ohne dass bei jeder entfernten Beobachtung eine neue Regressionsgleichung angepasst wird.

Formel

Notation

Begriff	Beschreibung
e_i	i-tes Residuum
h_i	i-tes Diagonalelement von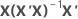
X	Versuchsplanmatrix
	i-ter angepasster Wert der Antwortvariablen
	angepasster Wert, berechnet ohne die i-te Beobachtung
MSE_(i)	mittlerer quadrierter Fehler, berechnet ohne die i-te Beobachtung
n	Anzahl der Beobachtungen
p	Anzahl der Modellparameter

Varianzinflationsfaktor (VIF)

Der VIF lässt sich durch Regression der einzelnen Prädiktoren auf die jeweils übrigen Prädiktoren und Aufzeichnen des R² berechnen.

Formel

Für Prädiktor x_j lautet der VIF:

Notation

Begriff	Beschreibung
R²( x_j)	Determinationskoeffizient mit x_j als Antwortvariable und den anderen Termen im Modell als Prädiktoren

Durbin-Watson-Statistik

Hiermit wird ein Test auf Autokorrelation in den Residuen durchgeführt, indem ermittelt wird, ob die Korrelation zwischen zwei benachbarten Fehlertermen null ist. Dieser Test basiert auf der Annahme, dass Fehler von einem autoregressiven Prozess erster Ordnung erzeugt werden. Minitab nimmt an, dass die Beobachtungen in einer sinnvollen Reihenfolge vorliegen, z. B. in zeitlicher Reihenfolge.

Zuerst multipliziert Minitab die Residuen mit der Quadratwurzel der Gewichtungen. Wenn Sie keine Gewichtungen verwenden, ist der Wert der Gewichtungen 1, und die gewichteten Residuen haben den gleichen Wert wie die normalen Residuen.

Die gewichteten Residuen werden in der folgenden Formel verwendet:

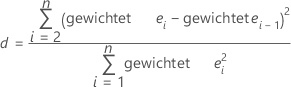
Notation

Begriff	Beschreibung
e_i	i-tes Residuum
e_{i – 1}	Residuum für die vorherige Beobachtung
n	Anzahl der Beobachtungen