In diesem Thema
Koeffizient (Koef)
Die Formel für den Koeffizienten oder die Steigung in der einfachen linearen Regression lautet:
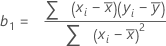
Die Formel für den Schnittpunkt mit der y-Achse (b0) lautet:

Ausgedrückt unter Verwendung von Matrizen lautet die Formel zum Berechnen des Vektors von Koeffizienten in der multiplen Regression:
b = (X'X)-1X'y
Notation
| Begriff | Beschreibung |
|---|---|
| yi | i-ter beobachteter Wert der Antwortvariablen |
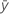 | Mittelwert der Antwortvariablen |
| xi | i-ter Prädiktorwert |
 | Mittelwert des Prädiktors |
| X | Designmatrix |
| y | Matrix der Antwortvariablen |
Standardfehler des Koeffizienten (SE Koef)
Bei der einfachen linearen Regression lautet der Standardfehler des Koeffizienten:
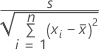
Die Standardfehler der Koeffizienten für die multiple Regression entsprechen den Quadratwurzeln der Diagonalelemente dieser Matrix:
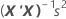
Notation
| Begriff | Beschreibung |
|---|---|
| xi | i-ter Prädiktorwert |
 | Mittelwert des Prädiktors |
| X | Designmatrix |
| X' | transponierte Designmatrix |
| s2 | Mittleres Fehlerquadrat |
t-Wert
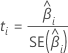
Notation
| Begriff | Beschreibung |
|---|---|
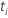 | Teststatistik für den  Koeffizienten Koeffizienten |
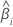 |  geschätzter Koeffizient geschätzter Koeffizient |
 | Standardfehler des  geschätzten Koeffizienten geschätzten Koeffizienten |
p-Wert – Koeffiziententabelle
Der beidseitige p-Wert für die Nullhypothese, dass ein Regressionskoeffizient gleich 0 ist, wird wie folgt ausgedrückt:
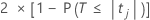
Die Freiheitsgrade sind die Freiheitsgrade für Fehler und werden wie folgt ausgedrückt:
n – p – 1
Notation
| Begriff | Beschreibung |
|---|---|
 | Kumulative Verteilungsfunktion der t-Verteilung mit Freiheitsgraden, die den Freiheitsgraden für Fehler entsprechen |
| tj | t-Statistik für den j-ten Koeffizienten |
| n | Anzahl der Beobachtungen im Datensatz |
| p | Die Summe der Freiheitsgrade für die Terme. Die Konstante zählt nicht zu den Termen. |
