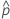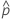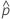In diesem Thema
R2 der Abweichung
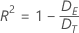
Notation
| Begriff | Beschreibung |
|---|---|
| DE | Error Deviance |
| DT | Total Deviance |
Korrigiertes R2 der Abweichung

Notation
| Begriff | Beschreibung |
|---|---|
| R2 | R2 der Abweichung |
| p | Freiheitsgrade der Regression |
| Φ | 1, für Binomial- und Poisson-Modelle |
| DT | Gesamtabweichung |
Obwohl die Berechnungen für das korrigierte R2 der Abweichung negative Werte ergeben können, wird in Minitab für derartige Fälle null angezeigt.
Akaike Information Criterion (AIC)
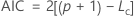
Die Log-Likelihood-Funktionen sind in Bezug auf die Mittelwerte parametrisiert. Die allgemeine Form der Funktionen lautet:
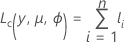
Die allgemeine Form der individuellen Beiträge lautet:

Die spezifische Form der individuellen Beiträge hängt vom Modell ab.
| Modell | li |
| Binomial | 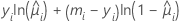 |
| Poisson |  |
Notation
| Begriff | Beschreibung |
|---|---|
| p | Freiheitsgrade der Regression |
| Lc | Log-Likelihood des aktuellen Modells |
| yi | Anzahl der Ereignisse für die i-te Zeile |
| mi | Anzahl der Versuche für die i-te Zeile |
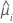 | geschätzter Mittelwert der Antwortvariablen für die i-te Zeile |
Akaikes korrigiertes Informationskriterium (AICc)

Das AICc wird nicht berechnet, wenn  .
.
Notation
| Begriff | Beschreibung |
|---|---|
| p | Anzahl der Koeffizienten im Modell einschließlich der Konstante |
| n | Anzahl der Datenzeilen ohne fehlende Daten |
Bayessches Informationskriterium (BIC)

Notation
| Begriff | Beschreibung |
|---|---|
| p | Anzahl der Koeffizienten im Modell, wobei die Konstante nicht gezählt wird |
| n | Anzahl der Datenzeilen ohne fehlende Daten |
R2 der Abweichung für Test
Formel
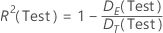
Hierbei stellt die folgende Gleichung die Fehlerabweichung dar:
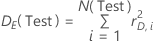
- Binär logistisch
-
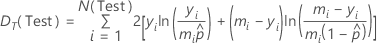
- Poisson
-

Notation
| Begriff | Beschreibung |
|---|---|
| N(Test) | Anzahl der Zeilen im Testdatensatz |
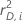 | quadrierte Abweichungsresiduen |
| yi | Anzahl der Ereignisse für die i-te Zeile im Testdatensatz |
| mi | Anzahl der Versuche für die i-te Zeile im Testdatensatz |
| DE(Test) | Fehlerabweichung für den Testdatensatz |
| DT(Test) | Gesamtabweichung für den Testdatensatz |
R2 der Abweichung für K Faltungen

Hierbei ist

und DT ist die Gesamtabweichung.
Notation
| Begriff | Beschreibung |
|---|---|
| K | Anzahl der Faltungen |
| nj | Stichprobenumfang der Faltung j |
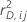 | Kreuzvalidiertes Residuum der Abweichung für die i-te Zeile der Faltung j |
Fläche unterhalb der ROC-Kurve
Formel


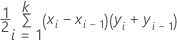
Hierbei ist k die Anzahl der eindeutigen Ereigniswahrscheinlichkeiten und (x0, y0) ist der Punkt (0, 0).
Um die Fläche für eine Kurve anhand eines Testdatensatzes oder von kreuzvalidierten Daten zu berechnen, verwenden Sie die Punkte aus der entsprechenden Kurve.
| x (Falsch-Positiv-Rate) | y (Richtig-Positiv-Rate) |
|---|---|
| 0,0923 | 0,3051 |
| 0,4154 | 0,7288 |
| 0,7538 | 0,9322 |
| 1 | 1 |
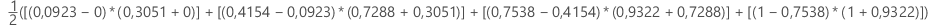

Notation
| Begriff | Beschreibung |
|---|---|
| TRP | Richtig-Positiv-Rate |
| FPR | Falsch-Positiv-Rate |
| TP | Richtig positiv; Ereignisse, die richtig bewertet wurden |
| P | Anzahl der tatsächlichen positiven Ereignisse |
| FP | Richtig negativ; Nicht-Ereignisse, die richtig bewertet wurden |
| N | Anzahl der tatsächlichen negativen Ereignisse |
| FNR | Falsch-Negativ-Rate |
| TNR | Richtig-Negativ-Rate |