In diesem Thema
Abweichung

Der Beitrag der einzelnen Datenpunkte zur skalierten Abweichung hängt vom Modell ab.
| Modell | Abweichung 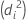 |
|---|---|
| Binomial | 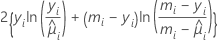 |
| Poisson | 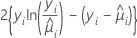 |
Die Freiheitsgrade für den Test hängen vom Stichprobenumfang und von der Anzahl der Terme im Modell ab:

Notation
| Begriff | Beschreibung |
|---|---|
| Lf | Log-Likelihood des vollständigen Modells |
| Lc | Log-Likelihood des Modells mit einer Teilmenge von Termen aus dem vollständigen Modell |
| yi | Anzahl der Ereignisse für die i-te Zeile in den Daten |
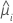 | geschätzter Mittelwert der Antwortvariablen für die i-te Zeile in den Daten |
| mi | Anzahl der Versuche für die i-te Zeile in den Daten |
| n | Anzahl der Zeilen in den Daten |
| p | Freiheitsgrade der Regression |
Pearson
Mit der verallgemeinerten Chi-Quadrat-Statistik nach Pearson wird die relative Differenz zwischen den beobachteten und den angepassten Werten ausgewertet.
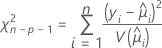
Die Freiheitsgrade für den Test hängen vom Stichprobenumfang und von der Anzahl der Terme im Modell ab. Die Pearson-Statistik weist für normalverteilte Daten exakt eine Chi-Quadrat-Verteilung auf. Bei nicht normalverteilten Daten, z. B. bei der Binomialverteilung und der Poisson-Verteilung, nähert sich die Statistik der Verteilung asymptotisch an.
Notation
| Begriff | Beschreibung |
|---|---|
| n | Anzahl der Zeilen in den Daten |
| p | Freiheitsgrade der Regression |
| yi | Wert der Antwortvariablen für das i-te Faktoren-/Kovariatenmuster |
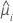 | geschätzter Mittelwert der Antwortvariablen für die i-te Zeile |
| V(·) | Varianzfunktion für das Modell, wie weiter unten definiert |
Die Varianzfunktion hängt vom Modell ab:
| Modell | Varianzfunktion |
|---|---|
| Binomial | 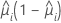 |
| Poisson | 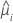 |
Hosmer-Lemeshow
Die Formel lautet wie folgt:
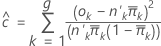
Um die Gruppen zu bilden, ordnet Minitab die geschätzten Wahrscheinlichkeiten der Größe nach an und versucht dann, 10 gleich große Gruppen zu erstellen.
Die erwartete Anzahl der Ereignisse in einer Gruppe beträgt:
erwartete Ereignisse = 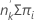
Der erwartete Wert für die Anzahl der Nicht-Ereignisse beträgt:
erwartete Nicht-Ereignisse = 
Notation
| Begriff | Beschreibung |
|---|---|
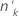 | Anzahl der Versuche in der k-ten Gruppe |
| ok | Anzahl der Ereignisse in den 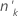 Faktoren-/Kovariatenmustern Faktoren-/Kovariatenmustern |
 | durchschnittliche geschätzte Wahrscheinlichkeit für jede Gruppe |
| πi | angepasste Wahrscheinlichkeiten für die Faktoren-/Kovariatenmuster in einer Gruppe |
