In diesem Thema
Koeffizienten
Es gibt zwei Methoden, um die Maximum-Likelihood-Schätzwerte für die Koeffizienten zu ermitteln. Eine Methode besteht darin, die Likelihood-Funktion in Bezug auf die Koeffizienten direkt zu maximieren. Diese Ausdrücke sind in den Koeffizienten nichtlinear. Die alternative Methode besteht darin, einen iterativ neu gewichteten Least Squares (IRWLS)-Ansatz zu verwenden, d. h. die Methode, die Minitab verwendet, um die Schätzungen der Koeffizienten zu erhalten. McCullagh und Nelder1 zeigen, dass die beiden Methoden gleichwertig sind. Die iterative Methode mit neu gewichteten kleinsten Quadraten ist jedoch leichter zu implementieren. Weitere Informationen finden Sie in [1].
Einstufige Approximierungsmethode für einige Fälle von k-falz Kreuzvalidierung
Für einige Großmusterausführungen mit vielen Kreuzvalidierungsfalten verwendet Minitab eine einstufige Annäherungsmethode im Kreuzvalidierungsalgorithmus, um die Berechnungszeit zu verringern (siehe Pregibon2 und Williams3). Für diese Entwürfe, anstatt das Trainingsmodell für eine Falte mit dem IRWLS-Algorithmus zu voller Konvergenz zu passen, stammen die Kreuzvalidierungsstatistiken für die Falte aus den Regressionsparametern aus dem ersten iterativen Schritt des Algorithmus.
Die folgende Tabelle zeigt, welche Designs Kreuzvalidierungsstatistiken aus der 1-Schritt-Annäherung erhalten.
| Stichprobenumfang (n) | Anzahl der Spalten in der Entwurfsmatrix (p) | Anzahl der Falten (k) |
|---|---|---|
| 200 < n ≤ 500 | 150 < p ≤ 300 | k > 200 |
| s > 300 | k > 100 | |
| 500 < n ≤ 1000 | 100 < p ≤ 300 | k > 300 |
| s > 300 | k > 150 | |
| 1000 < n ≤ 10,000 | p bei 50 | k > 1.000 |
| 50 < p ≤ 200 | k > 200 | |
| 200 < p ≤ 400 | k > 50 | |
| s > 400 | k > 10 | |
| 10,000 < n ≤ 50,000 | p bei 50 | k > 200 |
| 50 < p ≤ 200 | k > 100 | |
| s > 200 | k > 20 | |
| 50,000 < n ≤ 100,000 | p bei 50 | k > 100 |
| 50 < p ≤ 150 | k > 50 | |
| s > 150 | k > 20 | |
| n > 100.000 | Jeder Wert von p | k > 100 |
Einstufiger Annäherungsalgorithmus
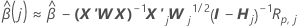
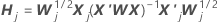
Notation
| Begriff | Beschreibung |
|---|---|
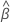 | die geschätzten Koeffizienten passen zum vollständigen Datensatz |
| X | die Entwurfsmatrix für den vollständigen Datensatz |
| X' | die Querung der Konstruktionsmatrix für den vollständigen Datensatz |
| W | die Gewichtsmatrix für den vollständigen Datensatz |
| X'j | die Konstruktionsmatrix für die Daten in der jth Falte |
| Wj | die Gewichtsmatrix für die Daten in der jth Falte |
| Ich | Identitätsmatrix |
| rp, j | der Vektor der Pearson-Residuen aus dem Modell für den vollständigen Datensatz für die Daten in der jth Falte |
[1] P. McCullagh und J. A. Nelder (1989). Generalized Linear Models, 2nd Ed., Chapman & Hall/CRC, London.
[2] D. Pregibon (1981). Logistische Regressionsdiagnose. The Annals of Statistics, 9(4), 705-724.
[3] D. A. Williams (1987). Generalisierte lineare Modelldiagnose mit Abweichung und Einzelfalllöschungen, Angewandte Statistik, 36(2), 181-191.
Standardfehler der Koeffizienten
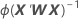
W ist eine Diagonalmatrix, bei der die Diagonalelemente mit der folgenden Formel angegeben werden:
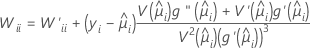
Dabei gilt Folgendes:

Diese Varianz-Kovarianz-Matrix beruht nicht auf der Fisher-Informationsmatrix, sondern auf der beobachteten Hesse-Matrix. Minitab verwendet die beobachtete Hesse-Matrix, da das resultierende Modell robuster gegenüber fehlerhaften Angaben der bedingten Mittelwerte ist.
Wenn die kanonische Linkfunktion verwendet wird, sind die beobachtete Hesse-Matrix und die Fisher-Informationsmatrix identisch.
Notation
| Begriff | Beschreibung |
|---|---|
| yi | Wert der Antwortvariablen für die i-te Zeile |
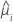 | geschätzter Mittelwert der Antwortvariablen für die i-te Zeile |
| V(·) | Varianzfunktion aus der folgenden Tabelle |
| g(·) | Linkfunktion |
| V '(·) | erste Ableitung der Varianzfunktion |
| g'(·) | erste Ableitung der Linkfunktion |
| g''(·) | zweite Ableitung der Linkfunktion |
Die Varianzfunktion hängt vom Modell ab:
| Modell | Varianzfunktion |
| Binomial | 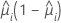 |
| Poisson | 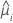 |
Weitere Informationen finden Sie unter [1] und [2].
[1] A. Agresti (1990). Categorical Data Analysis. John Wiley & Sons, Inc.
[2] P. McCullagh und J.A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
z
Mit der z-Statistik wird ermittelt, ob die Beziehung zwischen dem Prädiktor und der Antwortvariablen signifikant ist. Größere Absolutwerte von z weisen auf eine signifikante Beziehung hin. Die Formel lautet wie folgt:
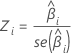
Notation
| Begriff | Beschreibung |
|---|---|
| Zi | Teststatistik für eine Standardnormalverteilung |
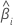 | Geschätzter Koeffizient |
 | Standardfehler des geschätzten Koeffizienten |
Bei kleinen Stichproben ist der Likelihood-Quotienten-Test möglicherweise zuverlässiger zum Erkennen der Signifikanz. Die p-Werte für den Likelihood-Quotienten befinden sich in der Abweichungstabelle. Wenn der Stichprobenumfang ausreichend groß ist, nähern sich die p-Werte für die z-Statistik den p-Werten für die Likelihood-Quotienten-Statistik an.
p-Wert (p)
p-Werte werden in Hypothesentests verwendet, um Ihnen die Entscheidung zu ermöglichen, ob eine Nullhypothese zurückgewiesen oder nicht zurückgewiesen werden sollte. Der p-Wert stellt die Wahrscheinlichkeit dar, eine Teststatistik zu erhalten, die mindestens so extrem wie der tatsächlich berechnete Wert ist, wenn die Nullhypothese wahr ist. Ein häufig verwendeter Trennwert für den p-Wert ist 0,05. Wenn beispielsweise der berechnete p-Wert einer Teststatistik kleiner als 0,05 ist, weisen Sie die Nullhypothese zurück.
Chancenverhältnisse für eine binäre logistische Regression
Das Chancenverhältnis wird nur ausgegeben, wenn Sie für ein Modell mit einer binären Antwortvariablen die Logit-Linkfunktion auswählen. In diesem Fall ist das Chancenverhältnis hilfreich beim Interpretieren der Beziehung zwischen einem Prädiktor und einer Antwortvariablen.
Der Wert für das Chancenverhältnis (τ) kann jede nicht negative Zahl sein. Das Chancenverhältnis = 1 dient als Basis für den Vergleich. Wenn τ = 1, besteht zwischen der Antwortvariablen und dem Prädiktor keine Assoziation. Wenn τ < 1, ist die Chance für das Ereignis auf der Referenzstufe des Faktors (oder auf niedrigeren Stufen eines stetigen Prädiktors) größer. Wenn τ > 1, ist die Chance für das Ereignis auf der Referenzstufe des Faktors (oder auf niedrigeren Stufen eines stetigen Prädiktors) kleiner. Je weiter ein Wert von 1 entfernt ist, desto stärker ist der Grad der Assoziation.
Hinweis
Für das binäre logistische Regressionsmodell mit einer Kovariate oder einem Faktor beträgt die geschätzte Erfolgschance:
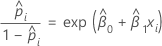
Die exponentielle Beziehung liefert eine Interpretation für β: Die Chance steigt bei jeder Zunahme von x um eine Einheit multiplikativ um eβ1. Das Chancenverhältnis entspricht exp(β1).
Wenn β z. B. 0,75 beträgt, beträgt das Chancenverhältnis exp(0,75), also 2,11. Dies weist darauf hin, dass die Erfolgschance mit jeder Zunahme von x um eine Einheit um 111 % ansteigt.
Notation
| Begriff | Beschreibung |
|---|---|
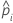 | geschätzte Wahrscheinlichkeit eines Erfolgs für die i-te Zeile in den Daten |
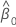 | geschätzter Koeffizient des Schnittpunkts mit der y-Achse |
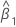 | geschätzter Koeffizient für Prädiktor x |
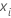 | Datenpunkt für die i-te Zeile |
Konfidenzintervall
Das Konfidenzintervall bei großen Stichproben für einen geschätzten Koeffizienten lautet:
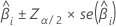
Bei der binären logistischen Regression stellt Minitab Konfidenzintervalle für die Chancenverhältnisse bereit. Um das Konfidenzintervall für das Chancenverhältnis zu erhalten, potenzieren Sie die Unter- und die Obergrenze des Konfidenzintervalls. Das Intervall gibt den Bereich an, in dem die Chance für jede Änderung des Prädiktors um eine Einheit liegen kann.
Notation
| Begriff | Beschreibung |
|---|---|
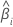 | i-ter Koeffizient |
 | inverse kumulative Wahrscheinlichkeit der Standardnormalverteilung bei 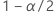 |
 | Signifikanzniveau |
 | Standardfehler des geschätzten Koeffizienten |
Varianz-Kovarianz-Matrix
Hierbei handelt es sich um eine d x d-Matrix, wobei d die Anzahl der Prädiktoren plus eins ist. Die Varianz jedes Koeffizienten befindet sich in der Diagonalzelle, und die Kovarianz jedes Koeffizientenpaars befindet sich in der entsprechenden nicht diagonalen Zelle. Die Varianz ist der quadrierte Standardfehler des Koeffizienten.
Die Varianz-Kovarianz-Matrix stammt aus der letzten Iteration der Umkehrung der Informationsmatrix. Die Varianz-Kovarianz-Matrix hat die folgende Form:
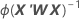
W ist eine Diagonalmatrix, bei der die Diagonalelemente mit der folgenden Formel angegeben werden:

Dabei gilt Folgendes:

Diese Varianz-Kovarianz-Matrix beruht nicht auf der Fisher-Informationsmatrix, sondern auf der beobachteten Hesse-Matrix. Minitab verwendet die beobachtete Hesse-Matrix, da das resultierende Modell robuster gegenüber fehlerhaften Angaben der bedingten Mittelwerte ist.
Wenn die kanonische Linkfunktion verwendet wird, sind die beobachtete Hesse-Matrix und die Fisher-Informationsmatrix identisch.
Notation
| Begriff | Beschreibung |
|---|---|
| yi | Wert der Antwortvariablen für die i-te Zeile |
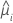 | geschätzter Mittelwert der Antwortvariablen für die i-te Zeile |
| V(·) | Varianzfunktion aus der folgenden Tabelle |
| g(·) | Linkfunktion |
| V '(·) | erste Ableitung der Varianzfunktion |
| g'(·) | erste Ableitung der Linkfunktion |
| g''(·) | zweite Ableitung der Linkfunktion |
Die Varianzfunktion hängt vom Modell ab:
| Modell | Varianzfunktion |
| Binomial | 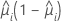 |
| Poisson | 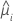 |
Weitere Informationen finden Sie in [1] und [2].
[1] A. Agresti (1990). Categorical Data Analysis. John Wiley & Sons, Inc.
[2] P. McCullagh und J.A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
